Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra học kì I (đề số 3) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho ABAM=ACAN. Giao tuyến của hai mặt phẳng (DBC) và (DMN) là
Hình chiếu song song của hai đường thẳng chéo nhau không thể có vị trí nào trong các vị trí tương đối sau?
Bảng dưới đây thống kê chiều cao của học sinh nữ lớp 12.
Chiều cao (cm) | Số học sinh | Giá trị đại diện |
[160;164) | 5 | 162 |
[164;168) | 6 | 166 |
[168;172) | 8 | 170 |
[172;176) | 2 | 174 |
[176;180) | 1 | 178 |
Chiều cao trung bình của học sinh nữ lớp 12 trên là
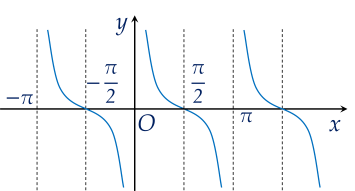
Hàm số có đồ thị trong hình nào dưới đây không liên tục tại x=1?
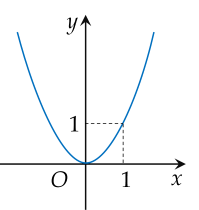
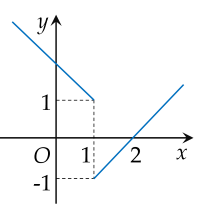
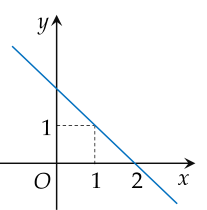
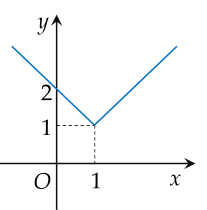
Giới hạn x→1+limx−13x−4 bằng
n→+∞limn2+17n2+5n+1954 bằng
Cho cấp số nhân (un) với u1=3 và u2=15. Công bội của cấp số nhân đã cho bằng
Cho dãy số (un) với un=sinnπ. Khi đó, dãy số (un)
Hàm số nào dưới đây có đồ thị là đường cong như hình vẽ?
Biết liman+29n2−3n+5−n=2,(a∈R). Giá trị của S=a2−1 là
Cho cấp số cộng (un), biết u21=−19;S22=0. Khi đó công sai d của cấp số cộng đó bằng
Cho dãy số (un) với {u1=1un+1=un+(−1)2n. Công thức tổng quát un nào sau đây là của dãy số đã cho?
Cho mẫu số liệu ghép nhóm sau:
| Điểm số môn Toán | Số học sinh đạt được |
| [0;2) | 1 |
| [2;4) | 6 |
| [4;6) | 12 |
| [6;8) | 14 |
| [8;10) | 8 |
| a) Cỡ mẫu của mẫu số liệu bằng 40. |
|
| b) Giá trị đại diện nhóm [2;4) bằng 3. |
|
| c) Độ dài nhóm [6;8) bằng 3. |
|
| d) Độ dài nhóm [8;10) bằng 2. |
|
Cho hình chóp S.ABC, gọi G,H lần lượt là trọng tâm các tam giác ΔABC và ΔSAB, M là trung điểm của AB. Lấy P là một điểm nằm trên cạnh BC khác B và C. Gọi Q là giao điểm của (PHG) và SB.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) CG∩(SAB)=M với M là trung điểm của SB. |
|
| b) GH // (SAC). |
|
| c) Gọi I là trọng tâm tam giác SAC. Khi đó SB // (HGI). |
|
| d) Tứ giác HGPQ là hình bình hành khi PBPC=3. |
|
Cho hàm số f(x)=x−1x2+ax+b và g(x)=x+a (a,b là các tham số).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Giới hạn của hàm số y=f(x) khi x→+∞ bằng 0. |
|
| b) Giới hạn của hàm số y=f(x)−g(x) khi x→−∞ bằng 1. |
|
| c) Nếu x→2limf(x)=−3 và x→2limg(x)=0 khi đó a=b. |
|
| d) Nếu x→1limf(x)=5 khi đó giá trị của biểu thức a+b=1. |
|
Người ta thiết kế một cái tháp gồm 15 tầng. Diện tích bề mặt của mỗi tầng bằng nửa diện
tích bề mặt của tầng ngay bên dưới và diện tích bề mặt của tầng 1 bằng nửa diện tích của
đế tháp.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Diện tích các tầng lập thành cấp số cộng có công sai d=21 |
|
| b) Diện tích các tầng lập thành cấp số nhân có công bội q=21 |
|
| c) Diện tích tầng 12 là 12,24(m2) |
|
| d) Cần 122564,2595m2 gạch để lát nền từ tầng 1 đến hết tầng 15. |
|
Thời gian (phút) di chuyển đến trường của nhóm học sinh trường THPT A được tổng hợp dưới bảng sau:
Thời gian (phút)
|
Số học sinh |
[15;20) | 6 |
[20;25) | 14 |
[25;30) | 25 |
[30;35) | 37 |
[35;40) | 13 |
[40;45) | 9 |
[45;50) | 21 |
Tìm trung vị của mẫu số liệu ghép nhóm trên? (làm tròn đến hàng phần mười)
Trả lời:
Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật ABCD.EFGH là hình chiếu của thùng hàng đó lên mặt đất với phương chiếu GM song song với các tia sáng mặt trời (các tia sáng mặt trời được xem là các đường thẳng song song với nhau), M trùng với điểm đối xứng với A qua D. Tính diện tích phần bóng râm được tô màu trong hình vẽ bên dưới, biết rằng BC=8 m, CD=2 m và CG=4 m. (kết quả tính theo đơn vị m2)
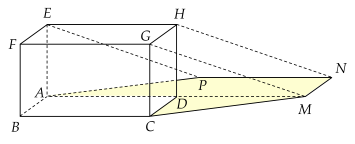
Trả lời:
Nếu hàm số y=f(x)=⎩⎨⎧x2+ax+bkhix<−5x+17khi−5≤x≤10ax+b+10khix>10 liên tục trên R thì a+b bằng bao nhiêu?
Trả lời:
Đoàn thanh niên xóm quyết định làm một số đèn lồng để tặng cho các em thiếu nhi tại địa phương trong dịp trung thu. Nguyên liệu làm đèn lồng cần dùng một số lượng giấy màu. Đoàn có tất cả 4 cuộn giấy màu đỏ, 6 cuộn giấy màu xanh, 4 cuộn giấy màu vàng và mỗi cuộn đều có độ dài 40 m. Ngày đầu tiên, Đoàn dùng hết 2 m giấy màu xanh, 1 m giấy màu đỏ và 0,5 m giấy màu vàng. Kể từ ngày thứ hai, mỗi ngày họ đều sử dụng hơn ngày trước đó 1 m giấy mỗi loại màu. Đoàn thanh niên quyết định làm đèn lồng cho đến khi tổng số giấy của cả ba màu còn lại 144 m thì xong. Đoàn thanh niên đó khi hoàn thành việc làm đèn lồng thì còn bao nhiêu mét giấy màu xanh?
Trả lời:
Chi phí (đơn vị: triệu đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x)=5x+12. Khi số sản phầm sản xuất ra càng lớn thì chi phí trung bình của mỗi sản phầm ngày càng giảm nhưng không vượt quá a triệu đồng. Giá trị nhỏ nhất của a là bao nhiêu?
Trả lời:
Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Sau 4 giờ, một tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?
Trả lời:
