Đề kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Hàm số nào sau đây luôn nghịch biến trên từng khoảng xác định của nó?

y=\dfrac{-x+1}{x-3}

.

y=\dfrac{3x+2}{5x+7}

.

y=\dfrac{-x+8}{x+3}

.

y=\dfrac{3x-1}{x+1}

.

Câu 2 (1đ):

Cho hàm số $y = f(x)$ có đạo hàm $f'(x)=x-1, \, \forall x\in \mathbb{R}$ . Số điểm cực trị của hàm số đã cho là

2

.

3

.

0

.

1

.

Câu 3 (1đ):

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như hình vẽ.

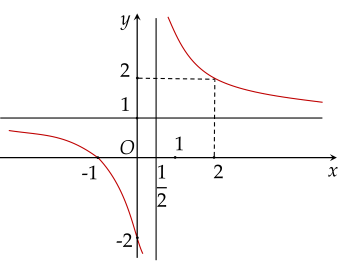
loading...

Điểm cực tiểu của đồ thị hàm số là

\left(4;2 \right)

.

\left(2;4 \right)

.

\left(0;2 \right)

.

\left(2;0 \right)

.

Câu 4 (1đ):

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-1;1]$ là đường cong như hình vẽ.

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-1;1]$

Gọi $M, \, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $f(x)$ trên đoạn $[-1;1]$ . Khi đó biểu thức $M-m$ bằng

2

.

4

.

3

.

0

.

Câu 5 (1đ):

Đồ thị hàm số $y=\dfrac{\sqrt{1-{{x}^{2}}}}{x-2}$ có bao nhiêu đường tiệm cận?

1

.

0

.

2

.

3

.

Câu 6 (1đ):

loading...

Hình vẽ trên là bảng biến thiên của hàm số nào sau đây?

y=-x^3-3x-2

.

y=x^3-3x^2-1

.

y=x^4+3x^2-1

.

y=-x^3+3x^2+2

.

Câu 7 (1đ):

Phương trình tiếp tuyến của đồ thị hàm số $y=x^3-3x^2+1$ tại điểm $A(3;1 )$ là

y=-9x-26.

y=9x-3.

y=-9x-3.

y=9x-26.

Câu 8 (1đ):

Số giao điểm của đồ thị hàm số $y=-\dfrac{x^4}{2}+x^2+\dfrac{3}{2}$ và trục hoành là

3

.

4

.

1

.

2

.

Câu 9 (1đ):

Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = f\left( x \right)=x+\dfrac{4}{x}$ trên đoạn $\left[ 1;3 \right]$ bằng

6

.

20

.

\dfrac{52}{3}

.

\dfrac{65}{3}

.

Câu 10 (1đ):

Tâm đối xứng của đồ thị hàm số $y=\dfrac{3x-7}{x+2}$ có tọa độ

(2;-3)

.

(-3;2)

.

(-2;3)

.

(3;-2)

.

Câu 11 (1đ):

Giá trị nhỏ nhất của hàm số $y=x-1+\dfrac{4}{x-1}$ trên khoảng $\left( 1;+\infty \right)$ là

4

.

3

.

2

.

5

.

Câu 12 (1đ):

Cho hàm số $y=\dfrac{x+5}{x+m}$ với $m$ là tham số.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Tập xác định của hàm số là $\mathbb{R}$ .
b) Với $m=2$ hàm số nghịch biến trên từng khoảng xác định.
c) Hàm số đồng biến trên từng khoảng xác định khi và chỉ khi $m>5$ .
d) Hàm số đồng biến trên khoảng $(-\infty ;-8)$ khi và chỉ khi $m\in [5;8]$ .

Câu 13 (1đ):

Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau.

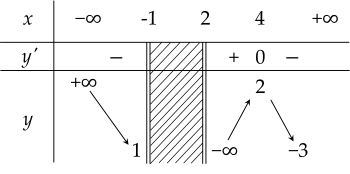
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số có giá trị cực đại bằng $3$ .
b) Hàm số có hai điểm cực trị.
c) Hàm số có giá trị lớn nhất bằng $1$ , nhỏ nhất bằng $-\dfrac{1}{3}$ .
d) Đồ thị hàm số không cắt trục hoành.

Câu 14 (1đ):

Cho hàm số $y=f(x)=\dfrac{{{x}^{2}}+2x+1}{x+3}\text{ }$ có đồ thị là $(C)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $y=f(x)=x-1+\dfrac{4}{x+3},\,\,\forall x\in (-\infty ;-3)\cup (-3;+\infty)$ .
b) Đồ thị $(C)$ không có tiệm cận ngang.
c) Đồ thị $(C)$ có tiệm cận đứng là đường thẳng $x=3$ .
d) Đồ thị $(C)$ có tiệm cận xiên là đường thẳng $y=ax+b$ . Khi đó ${{a}^{2}}+{{b}^{2}}=2.$

Câu 15 (1đ):

Trong $200$ gam dung dịch muối nồng độ $15\%$ , giả sử thêm vào dung dịch $x$ (gam) muối tinh khiết và được dung dịch có nồng độ $f(x)\%.$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số $f\left(x \right)=\dfrac{100(x+200)}{x+30}.$
b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng $(0; + \infty)$ .
c) Thêm càng nhiều gam muối tinh khiết thì nồng độ phần trăm càng tăng và không vượt quá $100\%$ .
d) Tiệm cận ngang của đồ thị hàm số $y = f(x)$ là $y = 100$ .

Câu 16 (1đ):

Cho hàm số $y=\dfrac{m{{x}^{2}}+\left(m+2 \right)x+5}{{{x}^{2}}+1}$ . Gọi $S$ là tập hợp các giá trị của $m$ sao cho đồ thị hàm số đã cho có đúng hai điểm cực trị và đường thẳng nối hai điểm cực trị của đồ thị hàm số cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng $\dfrac{25}{4}$ . Tính tổng giá trị các phần tử thuộc tập $S$ .

Trả lời:

Câu 17 (1đ):

Một bể chứa $1\,000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ $15$ gam muối cho mỗi lít nước với tốc độ $20$ lít/phút. Biết rằng nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số $f\left(t \right)$ , thời gian $t$ tính bằng phút. Phương trình tiệm cận ngang của đồ thị hàm số $y = f(t)$ là $y = a$ . Tính $a$ .

Trả lời:

Câu 18 (1đ):

Xét một chất điểm chuyển động dọc theo trục $Ox$ . Toạ độ của chất điểm tại thời điểm $t$ được xác định bởi hàm số $x(t)=t^3-6 t^2+9 t$ với $t \geq 0$ . Khi đó $x'(t)$ là vận tốc của chất điểm tại thời điểm $t$ , kí hiệu $v(t);\, v'(t)$ là gia tốc chuyển động của chất điểm tại thời điểm $t$ . Vận tốc của chất điểm giảm dần tới thời điểm $t_a$ lại bắt đầu tăng dần. Tính $t_a$ .

Trả lời:

Câu 19 (1đ):

Cho một tấm nhôm hình vuông có cạnh $24$ cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x$ (cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một khối hộp chữ nhật không nắp.

loading...

Tìm $x$ (đơn vị cm) sao cho thể tích khối hộp lớn nhất.

Trả lời:

Câu 20 (1đ):

Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức $G(x)=0,024x^2(30-x)$ , trong đó $x$ là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp ( $x$ được tính bằng mg). Tìm lượng thuốc $x$ tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Trả lời:

Câu 21 (1đ):

Cho hàm số $y=f\left(x \right)$ có đồ thị như hình bên dưới.

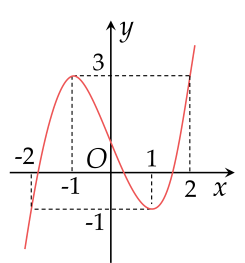
loading...

Phương trình $f'\big[f(x)-2\big]=0$ có bao nhiêu nghiệm?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP