Đề kiểm tra học kì I (đề số 2) chân trời sáng tạo

Câu 1 (1đ):

Bảng sau thống kê cân nặng của $30$ quả đu đủ được lựa chọn ngẫu nhiên sau khi thu hoạch ở vườn nhà Lan.

Cân nặng (g)	Số quả bưởi
$[750;800)$	$5$
$[800;850)$	$10$
$[850;900)$	$5$
$[900;950)$	$8$
$[950;1\,000)$	$2$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

250

.

1\,728,125

.

200

.

103,125

.

Câu 2 (1đ):

Trong không gian $Oxyz$ , biết $\overrightarrow{OM}=2\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}$ . Toạ độ của điểm $M$ là

(2;1;-3)

.

(-3;2;1)

.

(2;-3;1)

.

(-2;3;-1)

.

Câu 3 (1đ):

Phương trình tiếp tuyến của đồ thị hàm số $y=\dfrac{2x+1}{x-1}$ tại điểm có hoành độ $x=2$ là

y=-x+7

.

y=-3x+11

.

y=x-7

.

y=-3x+9

.

Câu 4 (1đ):

Các đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x-1}{\sqrt{4x^2+1}}$ là

y=1

;

y=-1

.

x=1

.

y=1

.

x= 1

;

x=-1

.

Câu 5 (1đ):

Cho hàm số $y=\sqrt[3]{(x^2-4)^2}$ có đồ thị như hình vẽ sau.

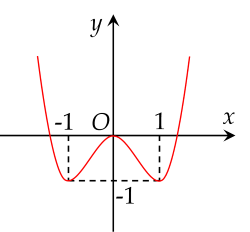
loading...

Khoảng nghịch biến của hàm số trên là

(-2; 2)

.

(-2; 0)

.

(2; +\infty)

.

(0; 2)

.

Câu 6 (1đ):

Khảo sát thời gian chơi thể thao trong một ngày của 40 học sinh lớp 10A giáo viên thu được một mẫu dữ liệu ghép nhóm như sau:

Thời gian (phút)	Số học sinh
$[30;40)$	$2$
$[40;50)$	$10$
$[50;60)$	$16$
$[60;70)$	$8$
$[70;80)$	$2$
$[80;90)$	$2$

Khoảng tứ phân vị của bảng số liệu ghép nhóm trên là

\Delta_Q = 14,5

.

\Delta_Q = 14

.

\Delta_Q = 17,5

.

\Delta_Q = 17

.

Câu 7 (1đ):

Trong không gian với hệ trục tọa độ $O x y z$ , cho tam giác $A B C$ có ba đỉnh $A(-1 ; 1 ;-3)$ , $B (4 ; 2 ; 1)$ , $C( 3 ; 0 ; 5)$ . Tọa độ trọng tâm $G$ của tam giác $A B C$ là

G (2 ; 1 ; 1).

G (3 ; 1 ; 1).

G (1 ; 3 ; 2).

G(-1 ; 2 ; 1).

Câu 8 (1đ):

Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị như sau:

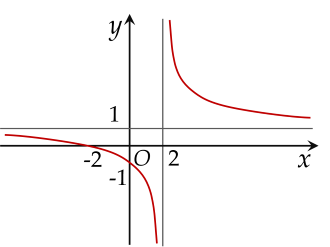
loading...

Mệnh đề nào sau đây đúng?

ad>0; \, bd<0

.

bc>0; \, ad<0

.

ac>0; \, bd>0

.

ab<0; \, cd<0

.

Câu 9 (1đ):

Để loại bỏ $x\%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là $C(x)=\dfrac{300x}{100-x}$ (triệu đồng), $0 \le x \le 100$ trong đó $C(x)$ là hàm số xác định trên $[ 0;100]$ . Đường tiệm cận đứng của đồ thị hàm số $y = C(x)$ là đường thẳng $x=x_0$ . Giá trị của $x_0$ là

-300

.

300

.

3

.

100

.

Câu 10 (1đ):

Giá trị lớn nhất của hàm số $y={{x}^{4}}-2{{x}^{2}}+3$ trên đoạn $\left[ 0;\sqrt{3} \right]$ là

M=6

.

M=9

.

M=8\sqrt{3}

.

M=1

.

Câu 11 (1đ):

Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là $a$ (m) ( $a$ chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi độ dài cạnh hình chữ nhật là dây cung của hình bán nguyệt).

Các kích thước (đơ vị mét) của nó để diện tích cửa sổ lớn nhất là

chiều rộng bằng

\dfrac{a}{4+\pi }

, chiều cao bằng

\dfrac{2a}{4+\pi }

.

chiều rộng bằng

\dfrac{2a}{4+\pi }

, chiều cao bằng

\dfrac{a}{4+\pi }

.

chiều rộng bằng

a(4-\pi)

, chiều cao bằng

2a(4-\pi)

.

chiều rộng bằng

a(4+\pi)

, chiều cao bằng

2a(4+\pi)

.

Câu 12 (1đ):

Cho hàm số $y=x^3-3x^2+5$ có đồ thị $(C)$ . Độ dài đoạn thẳng nối hai điểm cực trị của đồ thị $(C)$ bằng

5\sqrt{2}

.

2\sqrt{10}

.

2\sqrt{5}

.

10\sqrt{2}

.

Câu 13 (1đ):

Cho bảng số liệu ghép nhóm thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 – 2022 cho kết quả sau:

Số thẻ vàng	Tần số
$[40 ; 50)$	$2$
$[50 ; 60)$	$5$
$[60 ; 70)$	$7$
$[70 ; 80)$	$5$
$[80 ; 90)$	$0$
$[90 ; 100)$	$0$
$[100 ; 110)$	$1$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Cỡ mẫu của mẫu số liệu trên là $20.$
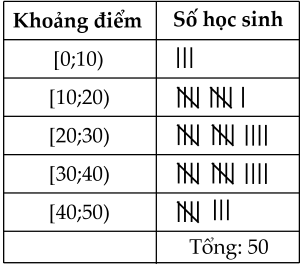
b) Khoảng biến thiên của mẫu số liệu trên là $50$ .
c) Tứ phân vị của thứ nhất của mẫu số liệu gốc thuộc vào nhóm $[50 ; 60)$ .
d) Khoảng tứ phân vị của mẫu số liệu trên là $\Delta_{Q}=26$ .

Câu 14 (1đ):

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ thỏa mãn $| \overrightarrow{a}|=2$ ; $| \overrightarrow{b}|=5$ , góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng $60^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $(\overrightarrow{a},\,-2\overrightarrow{b})=60^\circ$ .
b) $\overrightarrow{a}.\overrightarrow{b}=5$ .
c) $\| \overrightarrow{a}-2\overrightarrow{b}\|=84$ .
d) Biết vectơ $\overrightarrow{v}$ ngược hướng với vectơ $\overrightarrow{a}-2\overrightarrow{b}$ và $\| \overrightarrow{v} \|=4\sqrt{21}$ . Gọi $\alpha$ là góc giữa hai vectơ $\overrightarrow{v}$ và $\overrightarrow{a}$ . Khi đó $\cos \alpha =\dfrac{\sqrt{21}}{84}$ .

Câu 15 (1đ):

Cho hàm số $y=\dfrac{x^2-2x-3}{x-1}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số nhận đường thẳng $y=x+1$ làm tiệm cận xiên.
b) Hàm số có hai điểm cực trị.
c) Gọi $A,\, B, \, C$ là giao điểm của đồ thị hàm số với các trục $Ox,\, Oy$ . Diện tích tam giác $ABC$ bằng $6$ .
d) Có đúng hai giá trị nguyên của tham số $m$ để hàm số $f(x)=\dfrac{x^2-2x-3}{x-1}-m^2x$ đồng biến trên từng khoảng xác định.

Câu 16 (1đ):

Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau $t$ giờ $(t \geq 0)$ khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số $y(t)=5-\dfrac{15t}{9t^2+1}.$ (có đồ thị như đường màu cam ở hình bên)

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Vào thời điểm $t=1$ thì nồng độ oxygen trong nước là $3,5$ mg/l.
b) Nồng độ oxygen (mg/l) trong một hồ nước không vượt quá $5$ mg/l.
c) Vào thời điểm $t=0$ thì nồng độ oxygen trong nước cao nhất.
d) Nồng độ oxygen (mg/l) trong một hồ nước thấp nhất là $3,5$ mg/l.

Câu 17 (1đ):

Thành tích môn nhảy cao của các vận động viên tại một giải điền kinh dành cho học sinh trung học phổ thông như sau:

Mức xà (cm)	Số vận động viên
$[170;172)$	$3$
$[172;174)$	$10$
$[174;176)$	$6$
$[176;180)$	$1$

Tính độ lệch chuẩn của mẫu số liệu đã cho. (Làm tròn kết quả đến chữ số hàng phần trăm).

Trả lời: .

Câu 18 (1đ):

Cho hình hộp $A B C D . A' B' C' D'$ . Một đường thẳng $\Delta$ cắt các đường thẳng $A A', \, B C, \, C' D'$ lần lượt tại $M, \, N, \, P$ sao cho $\overrightarrow{N M}=2 \overrightarrow{N P}$ . Tính $\dfrac{M A}{M A'}$ .

Trả lời:

Câu 19 (1đ):

Trong hóa học cấu tạo của phân tử ammoniac $(NH_3)$ có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen $(N)$ và đáy là tam giác $H_1H_2H_3$ với $H_1,\,H_2,\,H_3$ là vị trí của ba nguyên tử hydrogen $(H)$ . Góc tạo bởi liên kết $H-N-H,$ có hai cạnh là hai đoạn thẳng nối $N$ với hai trong ba điểm $H_1,\,H_2,\,H_3$ (chẳng hạn như $\widehat{H_1NH_2}$ ) , được gọi là góc liên kết của phân tử $NH_3$ . Góc này xấp xỉ $120^{\circ }$ . Trong không gian $Oxyz,$ cho một phân tử $NH_3$ được biểu diễn bởi hình chóp tam giác đều $N.H_1H_2H_3$ với $O$ là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm $N$ thuộc trục $Oz$ , ba nguyên tử hydrogen ở các vị trị $H_1,\,H_2,\,H_3$ trong đó $H_1\left( 0;-\sqrt{3};0 \right)$ và $H_2H_3$ song song với trục $Ox$ . Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen. (làm tròn kết quả đến hàng phần trăm)

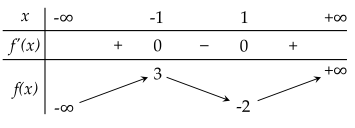
loading...

Trả lời:

Câu 20 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ , có đồ thị $(C )$ như hình vẽ sau:

loading...

Phương trình $| f(x) |=2$ có bao nhiêu nghiệm trên đoạn $[ 0;3 ]$ ?

Trả lời:

Câu 21 (1đ):

Hàm số $y=(x+m)^3+(x+n)^3-x^3$ đồng biến trên khoảng $(-\infty ;\,+\infty)$ . Giá trị nhỏ nhất của biểu thức $P=100[4(m^2+n^2)-m-n]$ bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Câu 22 (1đ):

Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số $y = h(x) = -\dfrac{1}{1\,320\,000}x^3 + \dfrac{9}{3\,520}x^2 -\dfrac{81}{44}x + 840$ với $0 \le x \le2\,000$ . Biết đỉnh của lát cắt dãy núi nằm ở độ cao $h$ (m) thuộc đoạn $[1\,000; 2\,000]$ . Tính $h$ . (Kết quả làm tròn đến hàng đơn vị)

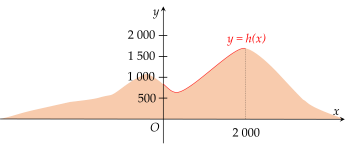
loading...

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP