Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì II (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x),y=g(x) liên tục và xác định trên R. Mệnh đề nào dưới đây đúng?
Họ nguyên hàm F(x) của hàm số f(x)=cos2x với hằng số C là
Hàm số F(x)=lnx+x+1 là một nguyên hàm của hàm số nào sau đây trên (0;+∞)?
Cho hàm số y=f(x) có đạo hàm liên tục trên [−2;3] thỏa mãn −2∫3f′(x)dx=8 và f(3)=12. Khi đó, f(−2) bằng
Tích phân 1∫2(x+3)2dx bằng
Nếu các số hữu tỉ a,b thỏa mãn 0∫1(aex+b)dx=e+2 thì giá trị của biểu thức a+b bằng
Trong không gian Oxyz, cho hai mặt phẳng (P):2x−3y+z−4=0; (Q):5x−3y−2z−7=0. Vị trí tương đối của (P) và (Q) là
Trong không gian Oxyz, cho mặt phẳng (P):1x+2y+3z=1. Khoảng cách từ gốc tọa độ O đến mặt phẳng (P) bằng
Một chiếc máy bay chuyển động trên đường băng với vận tốc v(t)=t2+10t (m/s) với t là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200(m/s) thì rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng dài bao nhiêu?
Trong hệ trục tọa độ Oxy, cho đồ thị hàm số y=f(x) như hình vẽ dưới đây và −3∫−1f(x)dx=5, −1∫1f(x)dx=−3. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox, đường thẳng x=−3;x=1 là

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):3x−ay+6z−10=0 và (Q):(b−1)x−y+2z−2022=0, với a,b∈R. Biết rằng mặt phẳng (P) song song với mặt phẳng (Q), giá trị biểu thức T=a+b là
Trong không gian Oxyz, hai mặt phẳng (P): x+2y−2z+3=0 và (Q): −x−2y+2z−12=0 lần lượt chứa hai mặt bên của một hình lập phương. Thể tích khối lập phương đó là
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;3;7);B(4;1;3). Gọi (α) là mặt phẳng trung trực của đoạn thẳng AB.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Mặt phẳng (α) đi qua điểm I(1;−1;−2). |
|
| b) Mặt phẳng (α) có vectơ pháp tuyến là n=(−1;1;2). |
|
| c) Phương trình mặt phẳng (α) có dạng ax+by+cz−9=0. Khi đó a+b+c=2. |
|
| d) Khoảng cách từ C(0;−1;2) đến mặt phẳng (α) là 66. |
|
Một mảnh đất hình chữ nhật có chiều dài 60m, chiều rộng 20m. Người ta muốn trồng cỏ ở hai đầu của mảnh đất và được giới hạn bởi hai đường Parabol có đỉnh cách nhau 40m (như hình vẽ dưới):

| a) Diện tích mảnh đất là 1200 m2. |
|
| b) Phương trình đường Parabol là y=x2+10. |
|
| c) Diện tích đất trồng cỏ là 800 m2. |
|
| d) Phần còn lại của mảnh đất người ta lát gạch với chi phí là 200000 đ/m2. Số tiền lát gạch là 186666667 (đồng). |
|
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t)=4t m/s, trong đó thời gian t tính bằng giây. Sau khi chuyển động được 10 giây thì ô tô gặp chuớng ngại vật và người tài xế phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với vận tốc v2(t) và gia tốc là a=−3 m/s2 cho đến khi dừng hẳn.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Quãng đường ô tô chuyển động nhanh dần đều là 200 m. |
|
| b) Vận tốc của ô tô tại thời điểm người tài xế phanh gấp là 40 m/s. |
|
| c) Thời gian từ lúc ô tô giảm tốc độ cho đến khi dừng hẳn là 40 giây. |
|
| d) Tổng quãng đường ô tô chuyển động từ lúc xuất phát đến khi dừng hẳn là khoảng 650,7 m. |
|
Hướng tới kỉ niệm ngày thành lập trường Đoàn TNCS Hồ Chí Minh. Khối 12 thiết kế bồn hoa gồm hai Elip bằng nhau có độ dài trục lớn bằng 8m và độ dài trục nhỏ bằng 4m đặt chồng lên nhau sao cho trục lớn của Elip này trùng với trục nhỏ của Elip kia và ngược lại (như hình vẽ):
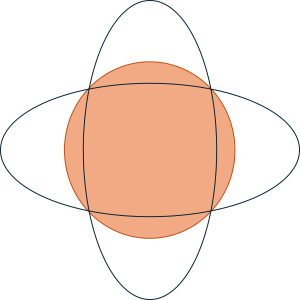
Phần diện tích nằm trong đường tròn đi qua 4 giao điểm của hai Elip dùng để trồng cỏ, phần diện tích bốn cánh hoa nằm giữa hình tròn và Elip dùng để trồng hoa.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Phương trình Elip nhận trục Ox là trục lớn là (E2):4x2+16y2=1. |
|
| b) Phương trình đường tròn đi qua 4 giao điểm của (E1) và (E2) là đường tròn có bán kính R=452. |
|
| c) Diện tích của 4 cánh hoa là 15 m2. |
|
| d) Biết kinh phí để trồng hoa là 150.000đồng/1m2, kinh phí để trồng cỏ là 100.000đồng/1m2. Tổng số tiền dùng để trồng hoa và trồng cỏ xấp xỉ 4 309 000(đồng). |
|
Một ô tô đang chạy thì gặp chướng ngại vật, người lái đạp phanh, từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc v(t)=−5t+20 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
Trả lời:
Cho f(x)={4x+1khix≥13x2+2khix<1. Giả sử F(x) là nguyên hàm của f(x) trên R thỏa mãn F(0)=2. Tính F(−2)+3F(4).
Trả lời:
Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là 25 m/s, gia tốc trọng trường là 9,8 m/s2. Quãng đường viên đạn đi được từ lúc bắn cho đến khi chạm đất là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
Ông Đức muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía trên là một Parabol, chất liệu làm là inox. Giá 1 m2 vật tư và công làm là 1,3 triệu đồng. Ông Đức phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng đơn vị)?

Trả lời :
Trong không gian Oxyz, cho mặt phẳng (α):2x+3y+z+1=0. Gọi (P) là mặt phẳng song song với (α), cắt các tia Ox,Oy,Oz lần lượt tại các điểm A, B, C sao cho thể tích khối tứ diện OABC bằng 6. Tính khoảng cách từ gốc tọa độ O đến mặt phẳng (P) (kết quả làm tròn đến hàng phần mười).
Trả lời:
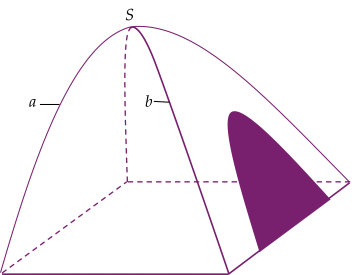
Một chiếc lều vải du lịch dạng hình cong như hình bên (lều bánh ú). Khung chính bao gồm đáy là hình vuông cạnh 2m và hai xương dây a, b nằm trên các đường parabol đỉnh S. Biết chiều cao của lều là SO=135cm, O là tâm của đáy. Thể tích chiếc lều bằng bao nhiêu (coi như độ dày của vải phủ và khung chính không đáng kể)?
Trả lời:
