Đề kiểm tra học kì I (đề số 1) chân trời sáng tạo

Câu 1 (1đ):

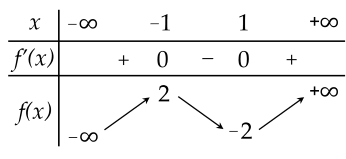
Cho bảng biến thiên của hàm số $y=f(x)$ , hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau đây?

(-1;1)

.

(1; 2)

.

(-2;0)

.

(0;1)

.

Câu 2 (1đ):

Hàm số $y=x^4-4x^2+4$ đạt cực tiểu tại những điểm nào?

x=\pm \sqrt{2}, \, x=0

.

x=-\sqrt{2}

.

x=\pm \sqrt{2}

.

x=\sqrt{2}, \, x=0

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?

\underset{[-3;2]}{\mathop{\max}} f(x)=3

.

\underset{[-3;2]}{\mathop{\max}} f(x)=-2

.

\underset{[-3;2]}{\mathop{\max}} f(x)=2

.

\underset{[-3;2]}{\mathop{\max}} f(x)=1

.

Câu 4 (1đ):

Phương trình tiếp tuyến của đồ thị hàm số $y=\dfrac{2x+1}{x-1}$ tại điểm có hoành độ $x=2$ là

y=-x+7

.

y=-3x+11

.

y=x-7

.

y=-3x+9

.

Câu 5 (1đ):

Trong không gian $Oxyz$ , cho hai điểm $A(2 ; 3 ; 4)$ và $B(3 ; 0 ; 1)$ . Độ dài của vectơ $\overrightarrow{A B}$ bằng

\sqrt{13}.

\sqrt{19}.

19 .

13 .

Câu 6 (1đ):

Trong không gian $Oxyz$ , cho vectơ $\overrightarrow{a}=( 2;\,-1;\,5)$ . Tọa độ vectơ $-5\overrightarrow{a}$ là

\left( -10;\,5;\,-25 \right)

.

\left( 10;\,-5;\,25 \right)

.

\left( 7;\,4;\,10 \right)

.

\left( -3;\,6;\,0 \right)

.

Câu 7 (1đ):

Bảng sau cho biết kết quả điều tra về chiều cao của học sinh khối lớp $10$ .

Chiều cao (cm)	Số học sinh
$[150;152)$	$5$
$[152;154)$	$18$
$[154;156)$	$40$
$[156;158)$	$26$
$[158;160)$	$8$
$[160;162)$	$3$

Khoảng biến thiên của mẫu số liệu trên là

10

.

16

.

15

.

12

.

Câu 8 (1đ):

Giá trị nhỏ nhất của hàm số $y=\dfrac{1}{{{x}^{3}}}-\dfrac{1}{x}$ khi $x>0$ là

\dfrac{2\sqrt{3}}{9}

.

-\dfrac{2\sqrt{3}}{9}

.

0

.

-\dfrac{1}{4}

.

Câu 9 (1đ):

Gọi $I$ là giao điểm của hai đường tiệm cận của đồ thị hàm số $y=\dfrac{2x-3}{x+1}$ . Khi đó, điểm $I$ nằm trên đường thẳng có phương trình là

x-y+4=0

.

2x-y+2=0

2x-y+4=0

.

x+y+4=0

.

Câu 10 (1đ):

Cho hàm số $y=ax^3+b x^2+cx+d$ $(a \ne 0)$ có bảng biến thiên như sau:

Giá trị của biểu thức $S=a+b+c+d$ là

0

.

-2

.

2

.

1

.

Câu 11 (1đ):

Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát $2$ km về phía nam và $1$ km về phía đông, đồng thời cách mặt đất $0,5$ km. Chiếc thứ hai nằm cách điểm xuất phát $1$ km về phía bắc và $1,5$ km về phía tây, đồng thời cách mặt đất $0,8$ km. Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng $(Oxy)$ trùng với mặt đất với trục $Ox$ hướng về phía nam, $Oy$ hướng về phía đông, $Oz$ hướng thẳng đứng lên trời, đơn vị đo ki-lô-mét.

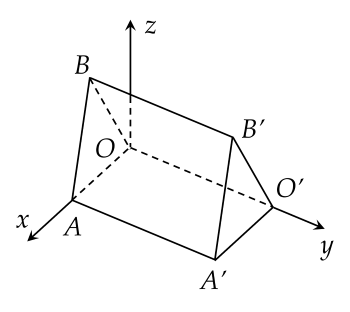
loading...

Khoảng cách giữa hai chiếc khinh khí cầu bằng

3,92

km.

3,82

km.

3,72

km.

3,62

km.

Câu 12 (1đ):

Thời gian chờ khám bệnh của các bệnh nhân tại phòng khám X được cho trong bảng sau:

Thời gian (phút)	Số bệnh nhân
$[0;5)$	$3$
$[5;10)$	$12$
$[10;15)$	$15$
$[15;20)$	$8$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm này (làm tròn đến chữ số hàng phần trăm) là

14,5

phút.

6,79

phút.

7,71

phút.

38

phút.

Câu 13 (1đ):

Số lượng xe máy điện bán được của một cửa hàng bán xe máy điện trong địa bàn thành phố Vinh trong tháng thứ $x$ được tính theo công thức $f\left(x \right)=50-\dfrac{30}{2+x}$ , trong đó $x\ge 1$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số lượng xe máy điện của cửa hàng được bán ra trong tháng đầu là $40$ xe.
b) Từ tháng thứ ba trở đi thì số lượng xe bán ra trong tháng đạt mức lớn hơn hoặc bằng $45$ xe/tháng
c) Nếu xem $y=f(x)$ là một hàm số xác định trên $\left[ 1;+\infty \right)$ thì đường tiệm cận ngang của đồ thị hàm số $y=f(x)$ là $y=0$ .
d) Khi $x$ càng lớn thì số lượng xe bán ra càng tiến gần đến mức $50$ xe/tháng.

Câu 14 (1đ):

Cho hàm số $y=\dfrac{x^2-2x-3}{x-1}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số nhận đường thẳng $y=x+1$ làm tiệm cận xiên.
b) Hàm số có hai điểm cực trị.
c) Gọi $A,\, B, \, C$ là giao điểm của đồ thị hàm số với các trục $Ox,\, Oy$ . Diện tích tam giác $ABC$ bằng $6$ .
d) Có đúng hai giá trị nguyên của tham số $m$ để hàm số $f(x)=\dfrac{x^2-2x-3}{x-1}-m^2x$ đồng biến trên từng khoảng xác định.

Câu 15 (1đ):

Cho tứ diện $ABCD$ có $AB\,=\,AC=AD=BC=BD=a$ , $\Delta BCD$ vuông cân tại $B$ . Gọi $M$ , $N$ lần lượt là trung điểm các cạnh $AB$ , $CD$ .

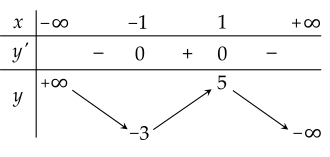
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{DB}$ .
b) $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$ .
c) $\overrightarrow{AB}.\overrightarrow{BC}=\dfrac{1}{2}{a^2}$ .
d) $(\overrightarrow{AD},\overrightarrow{BC})=120^\circ$ .

Câu 16 (1đ):

Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:

Thu nhập	Số người của nhà máy A	Số người của nhà máy B
$[5;8)$	$20$	$17$
$[8;11)$	$35$	$23$
$[11;14)$	$45$	$30$
$[14;17)$	$35$	$23$
$[17;17)$	$20$	$17$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nhà máy $A$ có số lượng người lao động nhiều hơn nhà máy $B.$
b) Mức thu nhập trung bình của người lao động ở hai nhà máy này bằng nhau.
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm của mẫu số liệu thu nhập của người lao động nhà máy $A$ nằm trong khoảng $(5;5,5)$ .
d) Xét theo khoảng tứ phân vị, ta thấy mức thu nhập của số người nhà máy $A$ phân tán hơn so với mức thu nhập của số người nhà máy $B.$

Câu 17 (1đ):

Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số $y = h(x) = -\dfrac{1}{1\,320\,000}x^3 + \dfrac{9}{3\,520}x^2 -\dfrac{81}{44}x + 840$ với $0 \le x \le2\,000$ . Biết đỉnh của lát cắt dãy núi nằm ở độ cao $h$ (m) thuộc đoạn $[1\,000; 2\,000]$ . Tính $h$ . (Kết quả làm tròn đến hàng đơn vị)

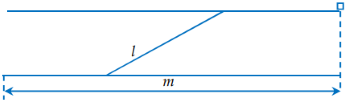
loading...

Trả lời:

Câu 18 (1đ):

Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và và có bảng biến thiên như sau:

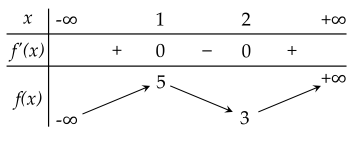
loading...

Phương trình $f(| x^2-2x | )=2$ có bao nhiêu nghiệm thực?

Trả lời:

Câu 19 (1đ):

Một công ty chuyên sản xuất dụng cụ thể thao nhận được đơn đặt hàng sản xuất $8\,000$ quả bóng rổ. Công ty có một số máy móc, mỗi máy có khả năng sản xuất $30$ bóng rổ trong một giờ. Chi phí thiết lập mỗi máy là $200$ nghìn đồng. Sau khi thiết lập, quá trình sản xuất sẽ diễn ra hoàn toàn tự động và chỉ cần có người giám sát. Chi phí trả cho người giám sát là $192$ nghìn đồng mỗi giờ. Công ty cần sử dụng bao nhiêu máy móc để chi phí hoạt động đạt mức thấp nhất?

Trả lời:

Câu 20 (1đ):

Cho tứ diện $A B C D$ . Gọi $M$ và $N$ lần lượt là trung điểm của $A B$ và $C D$ . Tìm giá trị $k$ trong đẳng thức vectơ $\overrightarrow{M N}=k(\overrightarrow{A D}+\overrightarrow{B C})$ . (ghi kết quả dưới dạng số thập phân)

Trả lời:

Câu 21 (1đ):

Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$ , mặt phẳng $(ABCD )$ song song với mặt phẳng nằm ngang. Khung sắt đó được đặt vào móc $E$ của chiếc cần cẩu sao cho các đoạn dây cáp $EA;\,EB;\,EC;\,ED$ bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc $\alpha$ .

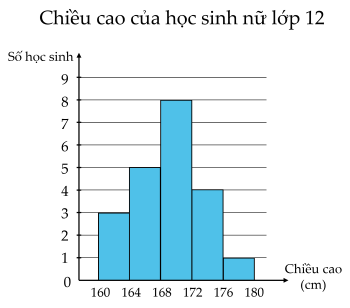
loading...

Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng $\overrightarrow{F_1};\,\overrightarrow{F_2};\,\overrightarrow{F_3};\,\overrightarrow{F_4}$ đều có cường độ là $4\,800\,\text{N}$ , trọng lượng của cả khung sắt chứa xe ô tô là $7\,200\sqrt{6}\,\text{N}$ . Tính $\sin \alpha$ . (làm tròn kết quả đến chữ số hàng phần trăm).

Trả lời:

Câu 22 (1đ):

Cho bảng mẫu số liệu ghép nhóm sau:

Nhóm	Tần số
$[20;26)$	$7$
$[26;32)$	$9$
$[32;38)$	$5$
$[38;44)$	$4$
$[44;50)$	$11$

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP