Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra số 1 (100% tự luận) SVIP
Sau khi điều tra số lần truy cập Internet của $40$ người trong vòng $1$ tuần (đơn vị: số lần truy cập), người ta có biểu đồ tần số ghép nhóm dưới đây:
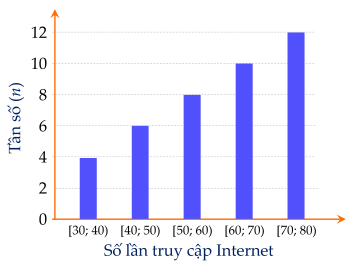
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm $[60; 70)$.
Hướng dẫn giải:
Tần số ghép nhóm của nhóm $[60; 70)$ là $10$.
Tần số tương đối ghép nhóm của nhóm $[60; 70)$ là $f_{[60;70)}=\dfrac{n_{[60;70)}}{N}=\dfrac{10}{40}.100\%=25\%$.
Một đĩa tròn bằng bìa cứng được chia làm $6$ phần bằng nhau và ghi các số $1, \, 2, \, 3, \, 4, \, 5, \, 6$. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa như hình vẽ dưới đây:
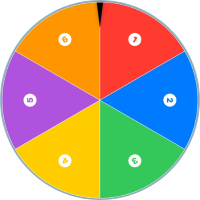
Xét phép thử "Quay đĩa tròn một lần". Tính xác suất của biến cố "Chiếc kim chỉ vào hình quạt ghi số chia hết cho $3$".
Hướng dẫn giải:
Xét phép thử $P$: "Quay đĩa tròn một lần".
Ta có số trường hợp của phép thử $P$ là: $n_P = 6$
Xét biến cố $A$: "Chiếc kim chỉ vào hình quạt ghi số chia hết cho $3$".
Ta có các trường hợp thuận lợi để biến cố $A$ xảy ra là : $3$; $6$.
Vậy $n(A) = 2$
Suy ra xác suất của biến cố $A$ là $P(A)=\dfrac{n(A)}{n_P}=\dfrac{2}{6}=\dfrac{1}{3}$.
Cho hai biểu thức $A=\dfrac{x}{\sqrt{x}+1}$; $B=\dfrac{3}{\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}+\dfrac{x+5}{x-1}$ với $x \ge 0, \, x \ne 1$.
a) Tính giá trị của $A$ tại $x=\dfrac14$.
b) Chứng minh rằng $B=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}$.
c) Đặt $P=A.B$. Tìm tất cả các giá trị của $x$ thỏa mãn $P\le 4$.
Hướng dẫn giải:
a) Thay $x=\dfrac14$ (thỏa mãn điều kiện) vào biểu thức $A$
$A=\dfrac{\dfrac14}{\sqrt{\dfrac14}+1}=\dfrac{\dfrac14}{\dfrac{1}{2}+1}=\dfrac{1}{6}$
Vậy với $x=\dfrac14$ thì giá trị của biểu thức $A=\dfrac{1}{6}$
b) $B=\dfrac{3}{\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}+\dfrac{x+5}{x-1}$
$=\dfrac{3}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}+\dfrac{x+5}{(\sqrt{x}+1)(\sqrt{x}-1)}$
$=\dfrac{3\sqrt{x}-3-\sqrt{x}-1+x+5}{(\sqrt{x}+1)(\sqrt{x}-1)}$
$=\dfrac{x+2\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-1)}$
$=\dfrac{(\sqrt{x}+1)^2}{(\sqrt{x}+1)(\sqrt{x}-1)}$
$=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}$
Vậy $B=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}$ (đpcm)
c) Ta có
$P=A.B=\dfrac{x}{\sqrt{x}+1}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{x}{\sqrt{x}-1}$.
$P \le 4$
$\dfrac{x}{\sqrt{x}-1}\le 4$
$\dfrac{x}{\sqrt{x}-1}-4\le 0$
$\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-1}\le 0$
$\dfrac{(\sqrt{x}-2)^2}{\sqrt{x}-1}\le 0\,$
TH1: $\dfrac{(\sqrt{x}-2)^2}{\sqrt{x}-1}=0\,$
$(\sqrt{x}-2)^2=0 $
$ x=4$ (tm).
TH2: $\dfrac{(\sqrt{x}-2)^2}{\sqrt{x}-1}<0$
$\sqrt{x}-1<0$ (do $\sqrt{x}-2)^2 \ge 0$)
$\sqrt{x}<1 $
$ x<1$.
Kết hợp với $x\ge 0,\, x\ne 1$ ta có $0\le x<1$và $x=4$ thì $P\le 4$.
Để chở hết $120$ tấn hàng ủng hộ đồng bào miền trung bị lũ lụt, một đội xe dự định dùng một số xe cùng loại. Lúc sắp khởi hành đội xe được bổ sung thêm $5$ xe cùng loại của các tình nguyện viên. Nhờ vậy mỗi xe phải chở ít đi $2$ tấn so với dự định. Lúc đầu đội có bao nhiêu xe, nếu khối lượng hàng của các xe phải chở là bằng nhau?
Hướng dẫn giải:
Gọi số xe theo dự định là $x $ chiếc ($x \in \mathbb{N}^*$)
Lượng hàng mỗi xe phải chở theo kế hoạch là: $\dfrac{120}{x}$ (tấn)
Do lúc sắp khởi hành đội được bổ sung thêm $5$ chiếc xe cùng loại nên suy ra: số xe thực tế chở là: $x + 5$ (chiếc)
Lượng hàng mỗi xe phải chở theo thực tế là: $\dfrac{120}{x+5}$ (tấn)
Theo bài ra ta có phương trình:
$\dfrac{120}{x}$ - $\dfrac{120}{x+5} = 2$
Biến đổi đưa về phương trình: $x^2 + 5x -300 = 0$
Giải phương trình được $x_1 = 15$, $x_2 = -20$
$x = -20$ không thỏa mãn (loại)
$x = 15$ (thỏa mãn)
Vậy số xe ban đầu là $15$ xe.
Trong tháng 7 năm 2024, hai hộ gia đình bác An và bác Bình dùng hết tổng cộng $500$ nghìn đồng tiền điện. Sang tháng 8 năm 2024, do tăng cường thực hiện việc sử dụng điện an toàn, tiết kiệm và hiệu quả; nhà bác An giảm được $15\%$ tiền điện và nhà bác Bình giảm được $10\%$ tiền điện; kết quả là cả hai hộ gia đình tiết kiệm được tổng cộng $65$ nghìn đồng tiền điện so tháng 7 năm 2024. Trong tháng 7 năm 2024, mỗi hộ gia đình dùng hết bao nhiêu đồng tiền điện?
Hướng dẫn giải:
Gọi số tiền điện hộ gia đình bác An trả trong 7/2024 là $x$ (nghìn đồng), $(0<x<500)$.
Gọi số tiền tiền điện hộ gia đình bác Bình trả trong tháng 7 năm 2024 là $y$ (nghìn đồng), $(0<y<500)$.
Số tiền điện hộ gia đình bác An được giảm trong tháng 8 năm 2024 là: $15\%x$ (nghìn đồng)
Số tiền điện hộ gia đình bác Bình được giảm trong tháng 8 năm 2024 là: $10\%y$ (nghìn đồng)
Theo đề bài ta có hệ phương trình:$\left\{ \begin{aligned}&x+y=500\,\,(1) \\&0,15x+0,1y=65\,\,(2) \\ \end{aligned} \right.$
Từ $(1)$ suy ra $y=500-x\,\,\,(3)$
Thay $(3)$ vào $(2)$ ta được $0,15x+0,1(500-x)=65$
$0,05x=15$
$x=300$ (nhận).
Thay $x=300$ vào $(3)$ ta được $y=200$ (nhận)
Vậy số tiền điện hộ gia đình bác Bình trả trong tháng 7 là $200$ nghìn đồng, gia đình bác An trả trong tháng 7 là $300$ nghìn đồng.
Cho phương trình $x^2-2(m-3)x-2(m-1)=0$. Tìm $m$ để phương trình có hai nghiệm phân biệt $x_1,\,x_2$ sao cho biểu thức $T=x_{1}^{2}+x_{2}^{2}$ đạt giá trị nhỏ nhất.
Hướng dẫn giải:
Có $\Delta '=[-(m-3)]^2-1.[-2(m-1)]=(m-3)^2+2m-2$
$\Delta '=m^2-4m+7=(m-2)^2+3>0,\,\forall m$
Do đó phương trình đã cho luôn có hai nghiệm phân biệt $x_1,\,x_2$
Theo định lí Viète, ta có: $x_1+x_2=\dfrac{-b}{a}=2(m-3);\,x_1.x_2=\dfrac{c}{a}=-2(m-1)$
Ta có: $T=x_{1}^{2}+x_{2}^{2}=(x_1+x_2)^2-2x_1x_2$
$T=[-2(m-3)]^2-2[-2(m-1)]$
$T=4m^2-20m+32=(2m-5)^2+7\ge 7$
Suy ra giá trị nhỏ nhất của $T$ bằng $7$ khi $m=\dfrac{5}{2}$
Vậy $m=\dfrac{5}{2}$ là giá trị cần tìm.
Một người cần xây một bể nước trên sân thượng của ngôi nhà để dự trữ nước sử dụng cho sinh hoạt gia đình, khi đó có hai mẫu thiết kế để lựa chọn:
Mẫu 1: Bồn chứa nước có dạng hình hộp đáy là hình vuông, có độ dài đường chéo là $4$ mét, chiều cao $2$ mét;
Mẫu 2: Bồn chứa nước có dạng hình trụ đường kính đáy là $4$ mét, chiều cao $2$ mét.
Người đó nên chọn mẫu thiết kế nào để dự trữ nước được nhiều nhất?
Hướng dẫn giải:
Theo mẫu 1:
Vì đáy bể là hình vuông có độ dài đường chéo là $4$ m nên diện tích đáy bể là: $S_1=4.4 \, : \, 2=8$ m2
Thể tích của bể theo mẫu 1 là: $V_1=S_1.h_1=8.2=16$ m3
Theo mẫu 2:
Bán kính đáy bể hình trụ là: $R=d \, : \, 2=4 \, : \, 2=2$ m
Thể tích của bể theo mẫu 2 là: $V_2=\pi.R^2.h_2=\pi2^2.2\approx 25,13$ m3
Vì $V_2>V_1$ nên người đó nên chọn xây theo mẫu thiết kế số 2 để có được bể dự trữ nước là nhiều nhất.
Cho đường tròn $(O)$ có đường kính $AB$. Gọi $M$ là một điểm thuộc đường tròn ($M$ khác $A$ và $B$). Tiếp tuyến đi qua $M$ cắt tiếp tuyến đi qua $B$ tại điểm $K$.
a) Chứng minh tứ giác $OMKB$ nội tiếp.
b) Chứng minh $OK \perp MB$.
c) Kẻ một đường thẳng đi qua $K$ cắt đường tròn $(O)$ tại $E$ và $F$ ($E$ nằm giữa $K$ và $F$), $OK$ cắt $BM$ tại $H$. Chứng minh $\widehat{EMK}=\widehat{MFE}$ và $\widehat{OFE}=\widehat{EHK}$.
Hướng dẫn giải:

a) Ta có $MK$, $BK$ là các tiếp tuyến của $(O)$
Suy ra $\widehat{OMK}=\widehat{OBK}=90^\circ $ (tính chất tiếp tuyến)
Suy ra $\Delta MKO$ vuông tại $M$, $\Delta OBK$ vuông tại $B$.
Dựng đường trung tuyến $MI$, $BI$ lần lượt trong $\Delta MKO,\,\Delta OBK$ với $I$ là trung điểm của $OK$.
Suy ra $IM=IO=IK=IB=\dfrac{1}{2}OK$ (tính chất đường trung tuyến trong tam giác vuông)
Suy ra các điểm $M$, $O$, $K$, $B$ đều nằm trên đường tròn $(I)$
Vậy tứ giác $MOBK$ là tứ giác nội tiếp.
b) Ta có $MK$, $BK$ là các tiếp tuyến của $(O)$ cắt nhau tại $K$.
Suy ra $KM = KB$ (tính chất hai tiếp tuyến cắt nhau)
Mà $KO$ là phân giác của $\widehat{MKB}$
Suy ra $KO$ đồng thời là đường cao trong $\Delta MKB$.
Vậy $OK \perp MB$
c)Chứng minh $\widehat{EMK}=\widehat{MFE}$
Ta có $OM = OE$ nên $\Delta OME$ cân tại $O$.
Dựng đường cao $ OP$ của $\Delta OME$
Suy ra $\Delta OPM$ vuông tại $P$
Do đó $\widehat{PMO}+\widehat{MOP}=90^\circ $
Mà $\widehat{PMO}+\widehat{EMK}=90^\circ $ ($MK$ là tiếp tuyến của đường tròn $(O)$)
Suy ra $\widehat{MOP}=\widehat{EMK}$
Mặt khác $OP$ là đường cao đồng thời là đường phân giác trong $\Delta OME$
Ta có: $\widehat{MOP}=\widehat{EMK}=\dfrac{1}{2}\widehat{MOE}$ (1)
Ta thấy $\widehat{MFE}$ và $\widehat{MOE}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung $ME$.
Suy ra $\widehat{MFE}=\dfrac{1}{2}\widehat{MOE}$ (2)
Từ (1) và (2) suy ra $\widehat{EMK}=\widehat{MFE}$ (đpcm)
*) Chứng minh $\widehat{OFE}=\widehat{EHK}$
Xét $\Delta OMK$ và $\Delta MHK$ có:
$\widehat{OMK}=\widehat{MHK}=90^\circ $
$\widehat{MKO}$ chung
Suy ra $\Delta OMK\backsim \Delta MHK$ (g.g)
Suy ra $\dfrac{OK}{MK}=\dfrac{MK}{HK}$ hay $M{{K}^{2}}=OK.HK$ (1)
Xét $\Delta MEK$ và $\Delta FMK$ có:
$\widehat{EMK}=\widehat{MFE}$ (cmt)
$\widehat{EKM}$ chung
Suy ra $\Delta MEK \backsim \Delta FMK$ (g.g)
Suy ra $\dfrac{EK}{MK}=\dfrac{MK}{FK}$ hay $M{{K}^{2}}=EK.FK$ (2)
Từ (1) và (2) suy ra $OK.HK=EK.FK$ hay $\dfrac{KF}{HK}=\dfrac{OK}{EK}$
Xét $\Delta OFK$ và $\Delta EHK$ có:
$\dfrac{KF}{HK}=\dfrac{OK}{EK}$ (cmt)
$\widehat{OKF}$ chung
Suy ra $\Delta OFK\backsim \Delta EHK$ (c.g.c)
Vậy $\widehat{OFE}=\widehat{EHK}$ (hai góc tương ứng) (đpcm).
Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật có đáy là hình vuông sao cho thể tích khối hộp được tạo thành là $8$ dm3 và diện tích toàn phần đạt giá trị nhỏ nhất. Độ dài cạnh đáy của mỗi hộp muốn thiết kế là bao nhiêu?
Hướng dẫn giải:
Gọi cạnh đáy, chiều cao của hình vuông lần lượt là: $x$ (dm); $h$ (dm), $(x; \, y>0)$
Ta có thể tích của hình hộp chữ nhật là: $V=x^2.h=8$
Suy ra $ h=\dfrac{8}{x^2}$
$S_{tp}=2x^2+4xh=2x^2+4x.\dfrac{8}{x^2}=2x^2+\dfrac{32}{x}$
Áp dụng BĐT Cauchy cho ba số dương ta được:
${{S}_{tp}}=2x^2+\dfrac{32}{x}=2x^2+\dfrac{16}{x}+\dfrac{16}{x}\ge 3.\sqrt[3]{2x^2.\dfrac{16}{x}.\dfrac{16}{x}}=24$
Dấu "=" xảy ra khi $2x^2=\dfrac{16}{x}$
$x=2$ (thỏa mãn).
Vậy độ dài cạnh đáy của hình hộp muốn thiết kế là: $2$ dm.
