Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra học kì I (đề số 3) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x) có đồ thị như hình vẽ.
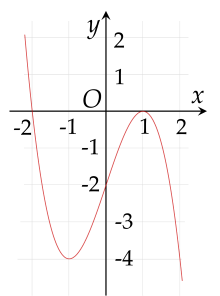
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số y=x4−4x2+4 đạt cực tiểu tại những điểm nào?
Hàm số nào dưới đây có bảng biến thiên như sau?

Trong không gian Oxyz, cho hai điểm A(1;2;3), B(−2;−4;9). Điểm M thuộc đoạn thẳng AB sao cho MA=2MB. Độ dài đoạn thẳng OM là
Cho bảng thống kê cân nặng của 30 học sinh lớp 12A1:
Cân nặng | Số học sinh |
[45;50) | 5 |
[50;55) | 10 |
[55;60) | 5 |
[60;65) | 8 |
[65;70) | 2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Giá trị của tham số m để giá trị nhỏ nhất của hàm số y=2x3−3x2+m trên đoạn [0;5] bằng 5 là
Tập giá trị của hàm số y=x−3+5−x là
Một công ty chuyên sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là: C(x)=2x+50 (triệu đồng), khi đó G(x)=xC(x) là chi phí sản xuất cho mỗi sản phẩm. Xem G(x) là một hàm số xác định trên [0;+∞), số tiệm cận ngang của đồ thị hàm số G(x) là
Cho hàm số y=x−1x2−x+1 có đồ thị (C). Biết tiếp tuyến song song với đường thẳng Δ:3x−4y+1=0, khi đó, phương trình tiếp tuyến của (C) là
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(−1;1;−3), B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
Số lượng đặt bàn của một nhà hàng được cho bởi bảng sau:
Số lượt | Tần số | Tần số tích lũy |
[1;6) | 14 | 14 |
[6;11) | 30 | 44 |
[11;16) | 25 | 69 |
[16;21) | 18 | 87 |
[21;26) | 5 | 92 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi bảng trên là
Kết quả đo chiều cao của 100 cây keo ba năm tuổi tại một nông trường được cho ở bảng sau:
| Chiều cao (m) | Số cây |
| [8,4;8,6) | 5 |
| [8,6;8,8) | 12 |
| [8,8;9,0) | 25 |
| [9,0;9,2) | 44 |
| [9,2;9,4) | 14 |
Phương sai của mẫu số liệu ghép nhóm đã cho (làm tròn đến chữ số hàng phần nghìn) bằng
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi hàm số có công thức c(t)=t2+1t (mg/L).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nồng độ thuốc trong máu của bệnh nhân sau 3 giờ là c(3)=103 (mg/L). |
|
| b) Đạo hàm của hàm số c(t)=t2+1t là c′(t)=(t2+1)21−t2. |
|
| c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng t∈(0;2). |
|
| d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi t=21. |
|
Cho hàm số y=mx2−2x+3x−1 có đồ thị (C).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Khi m=0, hàm số có tiệm cận ngang y=0. |
|
| b) Khi m=0, tọa độ giao điểm của hai đường tiệm cận thuộc đường thẳng x−y−2=0. |
|
| c) Đồ thị hàm số có một tiệm cận đứng khi m=2. |
|
| d) Gọi S là tập hợp các giá trị nguyên âm của m∈[−5;−1] để (C) có ba đường tiệm cận. Số phần tử của S là 1. |
|
Cho tứ diện OABC có các cạnh OA,OB,OC đôi một vuông góc và OA=OB=OC=a. Gọi M,N lần lượt là trung điểm các cạnh AB,OC.
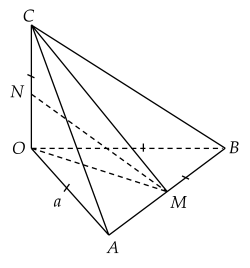
| a) MN=21(OA+BC). |
|
| b) cos(OM,CM)=33. |
|
| c) MN.OA=−2a2. |
|
| d) ∣CB+OA∣=a2. |
|
Bảng sau thống kê thời gian (đơn vị: phút) tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn Bình và bạn An.
| Thời gian (phút) |
Số ngày tập của Bình |
Số ngày tập của An |
| [15;20) | 5 | 5 |
| [20;25) | 10 | 5 |
| [25;30) | 10 | 15 |
| [30;35) | 2 | 3 |
| [35;40) | 1 | 0 |
| a) Khoảng biến thiên của mẫu số liệu về thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn An là 20 . |
|
| b) Khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn Bình là 28 . |
|
| c) Khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn An là 22. |
|
| d) Dựa vào khoảng tứ phân vị của hai mẫu số liệu trên thì thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn Bình phân tán hơn bạn An. |
|
Các bạn học sinh lớp 11A1 trả lời 40 câu hỏi trong một bải kiểm tra. Kết quả được thống kê ở bảng sau:
Số câu trả lời đúng | Số học sinh |
[16;21) | 4 |
[21;26) | 6 |
[26;31) | 8 |
[31;36) | 18 |
[36;41) | 4 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (Làm tròn kết quả đến chữ số hàng phần trăm)
Trả lời:
Cho hàm số y=f(x) có bảng biến thiên như sau:
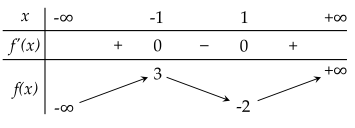
Phương trình ∣f(x)∣=2 có bao nhiêu nghiệm phân biệt?
Trả lời:
Một xí nghiệp A chuyên cung cấp sản phẩm S cho nhà phân phối B. Hai bên thỏa thuận rằng, nếu đầu tháng B đặt hàng x tạ sản phẩm S thì giá bán mỗi tạ sản phẩm S là P(x)=6−0,0005x2 (triệu đồng) (x≤40). Chi phí A phải bỏ ra cho x tạ sản phẩm S trong một tháng là C(x)=10+3,5x (triệu đồng) và mỗi sản phẩm bán ra phải chịu thêm mức thuế là 1 triệu đồng. Trong một tháng B cần đặt hàng bao nhiêu tạ sản phẩm S thì A có được lợi nhuận lớn nhất, kết quả làm tròn đến hàng phần mười.
Trả lời:
Trạm kiểm soát không lưu đang theo dõi hai máy bay. Giả sử trong không gian với hệ trục tọa độ Oxyz, đơn vị đo lấy theo kilômét, tại cùng một thời điểm theo dõi ban đầu: máy bay thứ nhất ở tọa độ A(0;35;10), bay theo hướng vector u1=(3;4;0), với tốc độ không đổi 900 km/h và máy bay thứ hai ở tọa độ B(31;10;11), bay theo hướng u2=(5;12;0) với tốc độ không đổi 910 (km/h). Biết khoảng cách an toàn tối thiểu giữa hai máy bay là 5 hải lý (khoảng 9,3 km). Nếu hai máy bay tiếp tục di chuyển với tốc độ bay như trên thì sau ít nhất bao nhiêu phút (kể từ thời điểm theo dõi ban đầu), hai máy bay vi phạm khoảng cách an toàn (kết quả làm tròn đến hàng phần trăm)?
Trả lời:
Trong không gian, cho hình lập phương ABCD.A′B′C′D′. Gọi N là điểm thỏa mãn C′N=2NB′, M là trung điểm của A′D′, I là giao điểm của A′N và B′M. Biết AI=aAA′+bAB+cAD. Tính a+b+c. (kết quả viết dưới dạng số thập phân)
Trả lời:
Tại một công ty sản xuất đồ chơi an toàn cho trẻ em, công ty phải chi 40000 USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi A, công ty phải trả 6 USD cho nguyên liệu ban đầu và nhân công. Gọi x, (x≥1) là số đồ chơi A mà công ty đã sản xuất và P(x) (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là F(x)=xP(x). Xem y=F(x) là hàm số theo x xác định trên nửa khoảng [1;+∞) có phương trình đường tiệm cận ngang là y=b. Tính b.
Trả lời:
