Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Dãy số nào sau đây không phải cấp số cộng ?

1;\,3;\,5\,;\,7\,;...

.

-1\,;\,-\dfrac{4}{5}\,;\,\,-\dfrac{3}{5}\,;\,-\dfrac{2}{5}\,;\,...

.

-2;-5 ;-3;2;...

.

-\dfrac{2}{3};-\dfrac{1}{3};0;\dfrac{1}{3}\,;\,....

.

Câu 2 (1đ):

Cho cấp số nhân với số hạng đầu $u_1=1$ và công bội $q=-3$ . Năm số hạng đầu của cấp số nhân đó là

1;-3;9;-27;81

.

1;-3;9;-27;51

.

1;-3;-9;-27;81

.

1;-3;9;27;-81

.

Câu 3 (1đ):

Cấp số nhân lùi vô hạn $(u_n)$ có $u_1=-2$ ; $q=\dfrac12$ . Tổng $S$ của cấp số nhân đã cho bằng

-\dfrac43

.

\dfrac43

.

4

.

-4

.

Câu 4 (1đ):

Hàm số $y = f(x)=\dfrac{x^2+1}{x^2-3x+2}$ liên tục trên khoảng nào sau đây?

(1;+\infty)

.

(-1;2)

.

(1;2)

.

(-\infty ; 2)

.

Câu 5 (1đ):

Gọi $i$ là nhóm có tần số lớn nhất. Gọi $u,\ g,\ {{n}_{i}}$ lần lượt là đầu mút trái, độ dài và tần số của nhóm $i$ ; $\ {{n}_{i-1}},\ \ {{n}_{i+1}}$ lần lượt là tần số của nhóm $i-1,\$ nhóm $i+1$ . Gọi $M_0$ là Mốt của mẫu số liệu ghép nhóm, mệnh đề nào sau đây đúng?

M_0=u+\left(\dfrac{{{n}_{i}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right).g

.

M_0=u+\left(\dfrac{{{n}_{i}}.{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i+1}}-{{n}_{i-1}}} \right).g

.

M_0=u.\left(\dfrac{{{n}_{i}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right)-g

.

M_0=u+\left(\dfrac{{{n}_{i+1}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right).g

.

Câu 6 (1đ):

Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Hình chiếu song song của điểm $A$ theo phương $AB$ lên mặt phẳng $(SBC)$ là điểm nào sau đây?

B

.

S

.

C

.

Trung điểm của

BC

.

Câu 7 (1đ):

Khẳng định nào sau đây sai?

A

Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng còn lại.

B

Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia.

C

Nếu mặt phẳng

(P)

chứa hai đường thẳng cùng song song với mặt phẳng

(Q)

thì

(P)

và

(Q)

song song với nhau.

D

Nếu hai mặt phẳng

(P)

và

(Q)

song song với nhau thì mặt phẳng

(R)

đã cắt

(P)

đều phải cắt

(Q)

và các giao tuyến của chúng song song nhau.

Câu 8 (1đ):

Quan sát một phần cầu thang như hình vẽ dưới đây:

hai đường thẳng chéo nhau

Khẳng định nào sau đây đúng?

b, \, d

chéo nhau.

a, \, d

cắt nhau.

a, \, b

cắt nhau.

a, \, d

chéo nhau.

Câu 9 (1đ):

Nghiệm của phương trình $\cot \left(3x-1 \right)=-\sqrt{3}$ là

x=\dfrac{1}{3}-\dfrac{\pi }{6}+k\pi, \, k\in \mathbb{Z}

.

x=\dfrac{1}{3}+\dfrac{\pi }{18}+\dfrac{k\pi }{3},\,k\in \mathbb{Z}

.

x=\dfrac{5\pi }{8}+\dfrac{k\pi }{3},\,k\in \mathbb{Z}

.

x=\dfrac{1}{3}+\dfrac{5\pi }{18}+\dfrac{k\pi }{3},\,k\in \mathbb{Z}

.

Câu 10 (1đ):

Cho dãy số $(a_n)$ với $a_n=\dfrac{7n+5}{kn+7} \, (k \in \mathbb{R})$ . Với giá trị nào của $k$ thì dãy số $(a_n)$ là dãy số tăng?

k>7

.

k<11

.

k<\dfrac{49}{5}

.

k>\dfrac{49}{5}

.

Câu 11 (1đ):

Cho cấp số cộng với số hạng thứ ba và số hạng thứ sáu trong cấp số cộng lần lượt là $5$ và $17$ . Công sai của cấp số cộng đó bằng

-3

.

4

.

7

.

12

.

Câu 12 (1đ):

$\underset{x \to +\infty }{\mathop{\lim}}(\sqrt{x^2+3x}-x-3)$ bằng

0

.

-\dfrac32

.

-3

.

-\dfrac72

.

Câu 13 (1đ):

Một bãi đỗ xe tính phí $60$ $000$ đồng cho giờ đầu tiên (hoặc một phần của giờ đầu tiên) và thêm $40$ $000$ đồng cho mỗi giờ (hoặc một phần của mỗi giờ) tiếp theo, tối đa là $200$ $000$ đồng.

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số $C=C(t)$ biểu thị chi phí theo thời gian đỗ xe.
b) Hàm số $C=C(t)$ liên tục trên $[0;+\infty)$ .
c) Từ đồ thị ta thấy $\underset{t\to 3}{\mathop{\lim}} C(t)=180 \, 000$ .
d) Một người có thời gian đỗ xe tăng dần đến $3$ giờ và một người có thời gian đỗ xe giảm dần đến $3$ giờ thì chênh lệch chi phí giữa hai người là $20\,000$ đồng.

Câu 14 (1đ):

Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

Khoảng điểm	Số học sinh
$\big[6,5 \, ; \, 7\big)$	$8$
$\big[7 \, ; \, 7,5\big)$	$10$
$\big[7,5 \, ; \, 8\big)$	$16$
$\big[8 \, ; \, 8,5\big)$	$24$
$\big[8,5 \, ; \, 9\big)$	$13$
$\big[9 \, ; \, 9,5\big)$	$7$
$\big[9,5 \, ; \, 10\big)$	$4$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Cỡ mẫu của mẫu số liệu là $n=80$ .
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: $Q_1=7,58$ .
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là: $Q_2=8,15$ .
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: $Q_3=8,63$

Câu 15 (1đ):

Cho tứ diện $ABCD$ . Các điểm $M$ , $N$ lần lượt là trung điểm của $AC$ , $BC$ , điểm $P$ thuộc đoạn $BD$ sao cho $BP = \dfrac23BD$ . Gọi $K$ là giao điểm của đường thẳng $AD$ và mặt phẳng $(MNP)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $KP$ // $AB$ .
b) Tứ giác $MNPK$ chỉ là hình thang không thể là hình bình hành.
c) Ba đường thẳng $KM$ , $NP$ , $CD$ đồng quy.
d) Gọi $I$ là giao điểm của $AP$ và $(DMN)$ thì $DI$ // $AB$ và $DI=\dfrac13AB$ .

Câu 16 (1đ):

Do nhu cầu đi lại của gia đình, anh Bình quyết định thực hiện tích góp tiền để mua một chiếc ôtô Vinfast VF8 trị giá $1,259$ tỉ đồng.

Đợt thứ nhất: anh Bình đã tích góp theo nguyên tắc tháng sau tích góp nhiều hơn tháng ngay trước đó số tiền là $2$ triệu đồng và cứ như thế đến tháng thứ $10$ anh phải góp $21$ triệu đồng. Đến hết đợt thứ nhất anh Bình có tất cả $624$ triệu đồng.

Đợt thứ hai kế tiếp: do muốn rút ngắn thời gian mua xe thì số tiền còn lại anh tiếp tục tích góp với tháng đầu là $5$ triệu đồng và mỗi tháng tiếp theo số tiền gấp đôi tháng kề trước nó.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đợt thứ nhất anh Bình tích lũy tiền theo dãy số là cấp số cộng có công sai là $d=2$ triệu đồng và $u_1=3$ triệu đồng.
b) Anh Bình tích lũy tiền hết đợt thứ nhất trong $25$ tháng.
c) Đợt thứ hai anh Bình tích lũy tiền theo dãy số là cấp số nhân có công bội là $q=2$ triệu đồng và $u_1=5$ triệu đồng.
d) Để đủ tiền mua ôtô thì anh Bình tích góp ít nhất $31$ tháng.

Câu 17 (1đ):

Chiều cao (đơn vị: m) của $35$ cây bạch đàn được cho ở bảng sau:

Số đo chiều cao (m)	Số cây
$\big[6,5 \, ; \, 7\big)$	$6$
$\big[7 \, ; \, 7,5\big)$	$9$
$\big[7,5 \, ; \, 8\big)$	$15$
$\big[8 \, ; \, 8,5\big)$	$4$
$\big[8,5 \, ; \, 9\big)$	$1$

Trung vị của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)

Trả lời:

Câu 18 (1đ):

Ở một công viên người ta trồng một số loài hoa hai bên đường từ cổng vào công viên sao cho các cây được trồng thẳng hai hàng dọc và khoảng cách giữa các cây ở mỗi hàng bằng $1$ mét. Họ trồng tất cả $10$ loài hoa trong đó có $100$ cây hoa cúc và $100$ cây hoa huệ. Những cây hoa cúc được trồng ở hàng bên phải, cây hoa cúc đầu tiên được trồng ở vị trí thứ tư của hàng và cứ cách $3$ cây hoa khác lại trồng $1$ cây hoa cúc. Những cây hoa huệ được trồng ở hàng bên trái, cây hoa huệ đầu tiên được trồng ở vị trí thứ nhất và cứ cách $5$ cây hoa khác lại trồng $1$ cây hoa huệ. Có bao nhiêu cặp cây hoa cúc và cây hoa huệ được trồng thẳng hàng ngang?

Trả lời:

Câu 19 (1đ):

Một kỹ sư mới ra trường làm việc với mức lương khởi điểm là $5 \, 000 \, 000$ đồng/tháng. Cứ sau $9$ tháng làm việc, mức lương của kỹ sư đó lại được tăng thêm $10\%$ . Sau $4$ năm làm việc tổng số tiền lương kỹ sư đó nhận được là bao nhiêu triệu đồng? Làm tròn đến hàng đơn vị

Trả lời:

Câu 20 (1đ):

Biết rằng $\underset{x \to +\infty }{\mathop{\lim}} \dfrac{(2-a)x-3}{x-\sqrt{x^2+1}}=+\infty$ (với $a$ là tham số). Giá trị nhỏ nhất của $P={{a}^{2}}-2a+4$ bằng bao nhiêu?

Trả lời:

Câu 21 (1đ):

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A,$ $\widehat{ABC}=60^\circ,$ $AB=8.$ Gọi $O, \, M$ lần lượt là trung điểm của $BC,AB.$ Mặt phẳng $(\alpha)$ qua $M$ và song song với $SB$ và $OA,$ cắt $BC, \, SC, \, SA$ lần lượt tại $N, \, P, \, Q.$ Tính diện tích của tứ giác $MNPQ$ , biết $SB \perp OA$ và $SB=8.$

Trả lời:

Câu 22 (1đ):

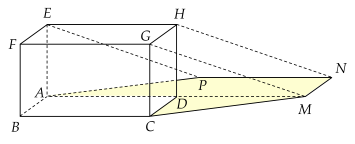
Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật $ABCD.EFGH$ là hình chiếu của thùng hàng đó lên mặt đất với phương chiếu $GM$ song song với các tia sáng mặt trời (các tia sáng mặt trời được xem là các đường thẳng song song với nhau), $M$ trùng với điểm đối xứng với $A$ qua $D$ . Tính diện tích phần bóng râm được tô màu trong hình vẽ bên dưới, biết rằng $BC=8$ m, $CD=2$ m và $CG=4$ m. (kết quả tính theo đơn vị m $^2$ )

Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP