olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Tải ma trận

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Hàm số nào dưới đây là hàm số lẻ?

y=tan⁡xy=\tan x.
y=cos⁡xy=\cos x.
y=sin⁡2xy={{\sin }^{2}}x.
y=cot⁡2xy={{\cot }^{2}}x.
Câu 2 (1đ):

Giá trị lớn nhất của hàm số y=3sin⁡xy=3\sin x là

33.
−3-3.
22.
11.
Câu 3 (1đ):

Nghiệm của phương trình 2cos⁡(x−15∘)−1=02\cos \left(x-15^\circ \right)-1=0 là

[x=60∘+k360∘x=−60∘+k360∘\left[ \begin{aligned} & x=60^\circ +k360^\circ \\ & x=-60^\circ +k360^\circ \\ \end{aligned} \right., k∈Zk\in \mathbb{Z}.
[x=75∘+k360∘x=−45∘+k360∘\left[ \begin{aligned} & x=75^\circ +k360^\circ \\ & x=-45^\circ +k360^\circ \\ \end{aligned} \right., k∈Zk\in \mathbb{Z}.
[x=75∘+k360∘x=135∘+k360∘\left[ \begin{aligned}& x=75^\circ +k360^\circ \\& x=135^\circ +k360^\circ \\ \end{aligned} \right., k∈Zk\in \mathbb{Z}.
[x=45∘+k360∘x=−45∘+k360∘\left[ \begin{aligned} & x=45^\circ +k360^\circ \\ & x=-45^\circ +k360^\circ \\ \end{aligned} \right., k∈Zk\in \mathbb{Z}.
Câu 4 (1đ):

Tập nghiệm của phương trình cot⁡ x=3\cot \ x=\sqrt{3} là

{π6+k2π ∣ k∈Z}\Big\{ \dfrac{\pi }{6}+k2\pi \, \big| \, k\in \mathbb{Z} \Big\}.
{−5π6+kπ ∣ k∈Z}\Big\{ \dfrac{-5\pi }{6}+k\pi \, \big| \, k\in \mathbb{Z} \Big\}.
{±π6+kπ ∣ k∈Z}\Big\{ \pm \dfrac{\pi }{6}+k\pi \, \big| \, k\in \mathbb{Z} \Big\}.
{π3+kπ ∣ k∈Z}\Big\{ \dfrac{\pi }{3}+k\pi \, \big| \, k\in \mathbb{Z} \Big\}.
Câu 5 (1đ):

Cho cấp số cộng (un)(u_n) có u1=3u_1=3 và u2=−1u_2=-1. Công sai của cấp số cộng đó bằng

−4-4.
44.
22.
11.
Câu 6 (1đ):

Cho dãy số (un)(u_n ) với un=sin⁡πnu_n=\sin \dfrac{\pi }{n}. Khi đó, dãy số (un)(u_n)

tăng.
bị chặn.
không bị chặn.
giảm.
Câu 7 (1đ):

Khẳng định nào sau đây đúng?

Hàm số y=cos⁡xy=\cos x là hàm số lẻ.
Hàm số y=sin⁡xy=\sin x là hàm số chẵn.
Hàm số y=cot⁡xy=\cot x là hàm số chẵn.
Hàm số y=tan⁡xy=\tan x là hàm số lẻ.
Câu 8 (1đ):

Tập giá trị của hàm số y=sin⁡2xy=\sin 2x là

[−1;1]\left[ -1;1 \right].
[0;2]\left[ 0;2 \right].
[−2;2]\left[ -2;2 \right].
R\mathbb{R}.
Câu 9 (1đ):

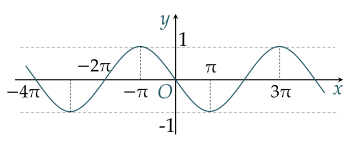
Đường cong trong hình vẽ là đồ thị của một trong bốn hàm số nào sau đây?

loading...

y=cos⁡x2y=\cos \dfrac{x}{2}.
y=−cos⁡x4y=-\cos \dfrac{x}{4}.
y=sin⁡x2y=\sin \dfrac{x}{2}.
y=sin⁡(−x2)y=\sin \Big(-\dfrac{x}{2} \Big).
Câu 10 (1đ):

Nghiệm của phương trình cos⁡2x−cos⁡x=0\cos^2 x-\cos x=0 thỏa mãn điều kiện 0<x<π0<x<\pi là

x=−π2x=-\dfrac{\pi }{2}.
x=π4x=\dfrac{\pi }{4}.
x=π6x=\dfrac{\pi }{6}.
x=π2x=\dfrac{\pi }{2}.
Câu 11 (1đ):

Cho một cấp số nhân có các số hạng đều không âm thỏa mãn u2=12 u_2=12 và u4=192 u_4=192 . Tổng của 9 9 số hạng đầu tiên của cấp số nhân đó là

1−49 1-4^9 .
−4(1−49) -4(1-4^9) .
49−1 4^9-1 .
4(1−49) 4(1-4^9) .
Câu 12 (1đ):

Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số sau đây?

loading...

y=cos⁡xy=\cos x.
y=sin⁡xy=\sin x.
y=cos⁡2xy=\cos 2x.
y=sin⁡2xy=\sin 2x.
Câu 13 (1đ):

Cho góc lượng giác xx, sao cho cos⁡x=−513\cos x=-\dfrac{5}{13} với 180∘<x<270∘180^\circ<x<270^\circ.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) sin⁡x<0\sin x<0.
b) tan⁡x=125\tan x=\dfrac{12}{5}.
c) cot⁡x=512\cot x=\dfrac{5}{12}.
d) sin⁡x−cos⁡x=−1213\sin x-\cos x=-\dfrac{12}{13}.
Câu 14 (1đ):

Chiều cao so với mực nước biển trung bình tại thời điểm tt của mỗi cơn sóng được cho bởi hàm số h(t)=75sin⁡(πt8)h(t)=75\sin \Big( \dfrac{\pi t}{8} \Big), trong đó h(t)h(t) được tính bằng centimét.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Chiều cao của sóng tại các thời điểm 55 giây bằng 69,369,3 cm.
b) Chiều cao của sóng tại các thời điểm 2020 giây bằng 7575 cm.
c) Trong 3030 giây đầu tiên, thời điểm để sóng đạt chiều cao lớn nhất là 66 giây.
d) Trong 3030 giây đầu tiên, có 33 thời điểm để sóng đạt chiều cao lớn nhất.
Câu 15 (1đ):

Giá của một chiếc xe ô tô lúc mới mua là 680680 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc xe ô tô giảm 5050 triệu đồng. Gọi unu_n là giá của chiếc ô tô trong năm thứ nn sử dụng.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) u2=630u_2=630.
b) Dãy số (un)(u_n) là cấp số cộng với công sai d=50d=50.
c) Giá của chiếc ô tô sau 33 năm sử dụng lớn hơn 500500 triệu đồng.
d) Sau ít nhất 88 năm sử dụng thì giá của chiếc ô tô nhỏ hơn một nửa giá trị ban đầu của nó.
Câu 16 (1đ):

Cho góc lượng giác xx, sao cho tan⁡x=13\tan x=\dfrac{1}{3} với π<x<3π2\pi <x< \dfrac{3\pi }{2}.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) cos⁡x<0\cos x<0.
b) cos⁡x=−1010\cos x=-\dfrac{\sqrt{10}}{10}.
c) sin⁡x=−1010\sin x=-\dfrac{\sqrt{10}}{10}.
d) sin⁡x+cos⁡x=−105\sin x+\cos x=-\dfrac{\sqrt{10}}{5}.
Câu 17 (1đ):

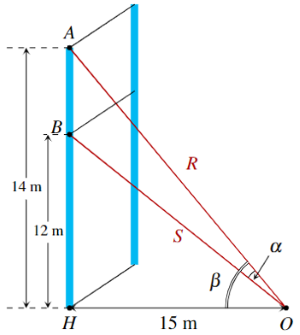
loading...

Cho tam giác ABCABC vuông tại AA có cạnh AB=6, AC=8AB=6, \, AC=8. Điểm EE thuộc đoạn ACAC sao cho CBE^=30∘\widehat{CBE}=30^\circ, điểm DD thuộc tia đối của tia BABA sao cho BCD^=30∘\widehat{BCD}=30^\circ. Tính độ dài đoạn ADAD. (làm tròn kết quả đến hàng phần mười)

Trả lời:

Câu 18 (1đ):

Số giờ có ánh sáng của một thành phố AA trong ngày thứ tt của năm 20252025 được cho bởi một hàm số y=4sin⁡∣π178(t−60)∣+10y=4\sin \Big| \dfrac{\pi }{178}( t-60) \Big|+10, với t∈Zt \in \mathbb{Z} và 60<t≤36560<t\le 365. Vào ngày thứ bao nhiêu trong năm đó thì thành phố AA có nhiều giờ ánh sáng mặt trời nhất?

Trả lời:

Câu 19 (1đ):

Cho dãy số (un)(u_n) biết un=an+5n+2u_n=\dfrac{an+5}{n+2}. Có bao nhiêu giá trị nguyên của aa nhỏ hơn 100100 để dãy số (un)(u_n) là dãy số tăng.

Trả lời:

Câu 20 (1đ):

Ông Sơn trồng cây trên một mảnh đất hình tam giác theo quy luật: ở hàng thứ nhất có 11 cây, hàng thứ hai có 22 cây, hàng thứ ba có 33 cây…, ở hàng thứ nn có nn cây. Biết rằng ông đã trồng hết 11 32511 \, 325 cây. Số hàng cây được trồng theo cách trên là bao nhiêu?

Trả lời:

Câu 21 (1đ):

Trong thời gian liên tục 25 25 năm, một người lao động luôn gửi đúng 4 000 000 4 \, 000 \, 000 đồng vào một ngày cố định của tháng ở ngân hàng M M với lãi suất không thay đổi trong suốt thời gian gửi tiền là 0,6% 0,6\% tháng. Gọi A A đồng là số tiền người đó có được sau 25 25 năm. Tính A A , đơn vị triệu đồng, làm tròn tới hàng đơn vị.

Trả lời:

Câu 22 (1đ):

Trong Vật lí, phương trình tổng quát của một vật dao động điều hoà cho bởi công thức x(t)=Acos⁡(ωt+φ)x(t)=A\cos (\omega t+\varphi), trong đó tt là thời điểm (tính bằng giây), x(t)x(t) là li độ của vật tại thời điểm t,At,A là biên độ dao động (A>0)(A>0) và φ∈[−π;π]\varphi \in [-\pi ;\pi ] là pha ban đầu của dao động. Xét hai dao động điều hoà có phương trình: x1(t)=3⋅cos⁡(π6t+π6){{x}_{1}}(t)=3\cdot \cos \left(\dfrac{\pi }{6}t+\dfrac{\pi }{6} \right) (cm) và x2(t)=3⋅cos⁡(π6t+π4){{x}_{2}}(t)=3\cdot \cos \left(\dfrac{\pi }{6}t+\dfrac{\pi }{4} \right) (cm). Từ dao động tổng hợp x(t)=x1(t)+x2(t)x(t)={{x}_{1}}(t)+{{x}_{2}}(t), sử dụng công thức biến đổi tổng thành tích ta tìm được pha ban đầu của dao động tổng hợp này bằng mπn\dfrac{m\pi }{n} với mn\dfrac mn là phân số tối giản có mẫu dương. Tính n−mn-m.

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP