Đề ôn tập và kiểm tra giữa học kì I toán 10 mới nhất

Câu 1 (1đ):

Công thức nào sau đây đúng?

S=\dfrac{1}{2}bc\sin B.

S=\dfrac{1}{2}bc\sin A.

S=\dfrac{1}{2}ac\sin A.

S=C\dfrac{1}{2}bc\sin C.

Câu 2 (1đ):

Giá trị $\cos 45^\circ + \sin 45^\circ$ bằng

\sqrt{3}

.

0

.

1

.

\sqrt{2}

.

Câu 3 (1đ):

Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned} & x-2y<0 \\ & x+3y>-2 \\ \end{aligned} \right.$ không chứa điểm nào sau đây?

(-1;0).

(0;3).

(-3;4)

.

(1;0).

Câu 4 (1đ):

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

\dfrac1{3}x-y^2<4

.

-x+5y\le 1

.

x^2-3y>0

.

x^2-y^2 \ge 0

.

Câu 5 (1đ):

Hình vẽ nào sau đây có phần không bị gạch minh họa cho tập hợp $\left(1;4 \right]$ ?

Câu 6 (1đ):

Cho tập hợp $A=\left\{ 1;2;3;4;x;y \right\}$ . Trong các mệnh đề sau, mệnh đề nào đúng?

(i): " $3\in A$ ";

(ii): " $\left\{ 3;4 \right\} \in A$ ";

(iii): " $\left\{ a;3;b \right\} \in A$ ".

(i) và (ii) đúng.

(i) và (iii) đúng.

(i) đúng.

(ii) và (iii) đúng.

Câu 7 (1đ):

Mệnh đề phủ định của mệnh đề "Phương trình $x^2+2x+5=0$ vô nghiệm" là

"Phương trình

x^2+2x+5=0

có nghiệm".

"Phương trình

x^2+2x+5=0

có hai nghiệm phân biệt".

"Phương trình

x^2+2x+5=0

không có nghiệm".

"Phương trình

x^2+2x+5=0

có nghiệm kép".

Câu 8 (1đ):

Giá trị của biểu thức $P=\sin 30^\circ. \cos 60^\circ + \sin 60^\circ. \cos 30^\circ$ là

P=0

.

P=1

.

P=\sqrt{3}

.

P=-\sqrt{3}

.

Câu 9 (1đ):

Cho hệ bất phương trình $\left\{ \begin{aligned} & x+y>0 \\ & 2x+5y<0 \\ \end{aligned} \right.$ có tập nghiệm là $S$ . Khẳng định nào sau đây đúng?

(1;1) \in S

.

\Big(-\dfrac12;\dfrac{2}{5}\Big) \in S

.

(-1;-1) \in S

.

\Big(1;-\dfrac12\Big) \in S

.

Câu 10 (1đ):

Cho tam giác $ABC$ có $AB=3, \, AC=6, \, \widehat{BAC}=60^\circ$ . Độ dài đường cao $h_a$ của tam giác $ABC$ bằng

\sqrt{3}.

\dfrac{3}{2}

.

3\sqrt{3}.

3.

Câu 11 (1đ):

Cho $\tan \alpha =2$ . Giá trị của $A=\dfrac{3\sin \alpha +\cos \alpha }{\sin \alpha -\cos \alpha }$ là

\dfrac{7}{3}

.

7

.

\dfrac{5}{3}

.

5

.

Câu 12 (1đ):

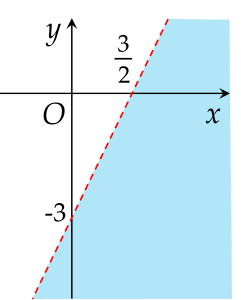
Phần tô màu trong hình vẽ (không bao gồm đường thẳng nét đứt) là miền nghiệm của bất phương trình nào sau đây?

loading...

x-2y<3

.

2x-y>3

.

x-2y>3

.

2x-y<3

.

Câu 13 (1đ):

Cho các hệ bất phương trình sau: $\left\{ \begin{aligned} &x-2y \le 0 \\&5x-y \ge -4 \\&x+2y \le 5 \\ \end{aligned} \right.$ , $\left\{ \begin{aligned} &-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right.$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned} &x-2y\le 0 \\ &5x-y\ge -4 \\ &x+2y\le 5 \\ \end{aligned} \right.$ là miền tam giác.
b) Điểm $M(1;1)$ thỏa mãn miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&x-2y\le 0 \\&5x-y\ge -4 \\&x+2y\le 5 \\ \end{aligned} \right.$ .
c) Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right.$ là miền tứ giác.
d) Điểm $O(0;0)$ không thỏa mãn miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\& y\le 6 \\ \end{aligned} \right.$ .

Câu 14 (1đ):

Cho hai tập hợp $A=\big\{ x\in \mathbb{R} \, \big| \, x+3<4+2x \big\}$ , $B=\big\{ x\in \mathbb{R} \, \big| \, 5x-3<4x-1 \big\}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A=\left(-1;\,+\infty \right).$
b) $B=\left(-\infty ;\,2 \right].$
c) $A \cap B=\left(-1;\,2 \right)$ .
d) Tập tất cả các số tự nhiên thuộc cả hai tập $A$ và $B$ là $\left\{ 0;1 \right\}.$

Câu 15 (1đ):

Cho $P(x)$ : " $x^2-x-2=0$ " với $x$ là các số thực.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $x=0$ thì $P(x)$ là mệnh đề đúng.
b) $P(-1)$ là mệnh đề sai.
c) $P(x)$ luôn là mệnh đề sai với $x$ là các số thực bất kì.
d) $P(2)$ là mệnh đề đúng.

Câu 16 (1đ):

Cho ba tập hợp: $A=\left(-\infty ;1 \right]$ ; $B=\left[ -2;2 \right]$ và $C=\left(0;5 \right)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $C \subset A$ .
b) $A \cap C=\left(0;1 \right]$ .
c) $A \cap B=\left( -2;1 \right)$ .
d) $\left(A\cap B \right) \cup \left(A\cap C \right)=\left[ -2;1 \right]$ .

Câu 17 (1đ):

Trong đợt khảo sát nghề, giáo viên chủ nhiệm lớp 10D đưa ra ba nhóm ngành cho học sinh lựa chọn, đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có $6$ học sinh chọn nhóm ngành Giáo dục, $9$ học sinh chọn nhóm ngành Y tế, $10$ học sinh chọn nhóm ngành Công nghệ thông tin, $22$ học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có $3$ học sinh chọn hai nhóm ngành Giáo dục và Y tế, $2$ học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, $3$ học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết lớp 10D có $40$ học sinh?

Trả lời:

Câu 18 (1đ):

Cho hai tập hợp khác rỗng $A=\left(m-3;5 \right]$ , $B=\left(-2;\,3m+1 \right)$ với $m\in \mathbb{R}$ . Tìm số nguyên $m$ lớn nhất để $A\subset B$ .

Trả lời:

Câu 19 (1đ):

Để chuẩn bị cho đại hội chi đoàn 10A1, bạn Nga được phân công đi mua hoa để cắm vào $3$ lọ, mỗi lọ cắm số hoa mỗi loại như nhau. Bạn Nga được lớp giao cho $200$ nghìn đồng để mua nhưng đến quầy bán chỉ còn $2$ loại hoa và đã mua đủ để cắm. Biết rằng một loại hoa có giá $15$ nghìn đồng/bông và một loại có giá $20$ nghìn/bông. Số tiền dư ra ít nhất có thể là bao nhiêu nghìn đồng?

Trả lời:

Câu 20 (1đ):

Cho $x, \, y$ thoả mãn hệ $\left\{ \begin{aligned} & x+2y-100 \le 0 \\ & 2x + y-80 \le 0 \\ & x \ge 0 \\ & y \ge 0 \\ \end{aligned} \right..$ Khi biểu thức $P=(x;y)=40 \, 000x+30 \, 000y$ đạt giá trị lớn nhất, tính $x+y$ .

Trả lời:

Câu 21 (1đ):

Một máy cán thép có thể sản xuất hai sản phẩm thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc $40$ giờ một tuần). Công suất sản xuất thép tấm là $250$ tấn/giờ, công suất sản xuất thép cuộn là $150$ tấn/giờ. Mỗi tấn thép tấm có giá $25$ USD, mỗi tấn thép cuộn có giá $30$ USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa $5$ $000$ tấn thép tấm và $3$ $500$ tấn thép cuộn. Cần sản xuất $m$ tấn thép tấm và $n$ tấn thép cuộn một tuần để lợi nhuận thu được là cao nhất. Tính $m - n$ .

Trả lời:

Câu 22 (1đ):

Để đo khoảng cách từ một điểm $A$ trên bờ sông đến gốc cây $C$ trên cù lao giữa sông, người ta chọn một điểm $B$ cùng ở trên bờ với $A$ sao cho từ $A$ và $B$ có thể nhìn thấy điểm $C$ . Ta đo được khoảng cách $AB=40$ m, $\widehat{CAB}=45^\circ$ và $\widehat{CBA}=70^\circ$ .

loading...

Sau khi đo đạc và tính toán ta được khoảng cách $AC$ bằng bao nhiêu mét? (làm tròn kết quả đến hàng phần mười)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP