Dạng 2. Xác định tiệm cận khi biết đồ thị hàm số hoặc bảng biến thiên SVIP

Một ứng dụng của hàm số trong vật lí là hệ số tương đối tính Lorentz được cho bởi công thức $\gamma (v)=\dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}$, với $v$ là vận tốc tương đối giữa các hệ quy chiếu quán tính, $c$ là tốc độ ánh sáng trong chân không. Hàm này được sử dụng trong thuyết tương đối đặc biệt của Einstein để mô tả các hiệu ứng tương đối tính có đồ thị dưới đây:

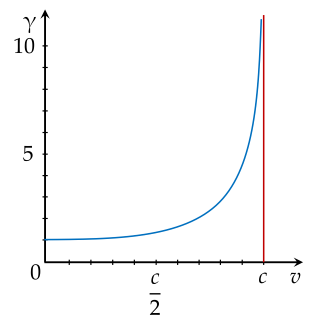
Đồ thị hàm số đó có tiệm cận đứng là

Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây.

Đồ thị hàm số $y=f(x)$ có bao nhiêu đường tiệm cận?

Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\backslash \left\{ -1;1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

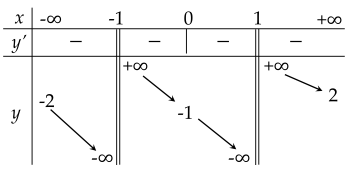
Số đường tiệm cận ngang của đồ thị hàm số $y=f(x)$ là

Cho đồ thị hàm số $y=f(x)$ có đồ thị như hình vẽ:

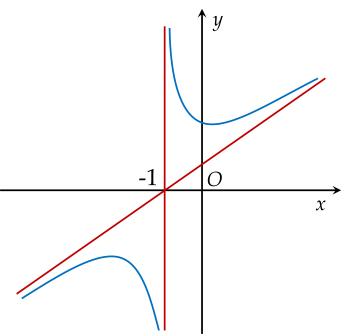
Tiệm cận đứng của đồ thị hàm số là đường thẳng

Cho hàm số $y=f(x )$có đồ thị như hình vẽ:

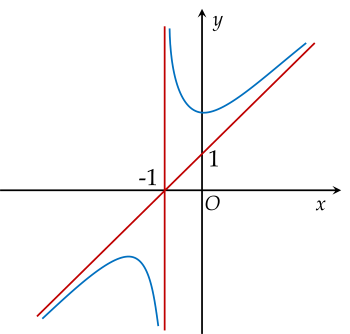
Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng

Hàm số nào sau đây có đồ thị như hình vẽ?

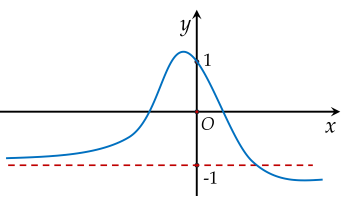
Hàm số nào sau đây có đồ thị như hình vẽ?

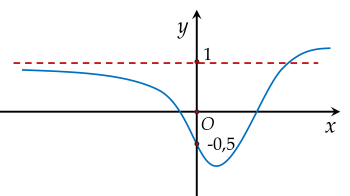
Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như sau:

Đồ thị hàm số $y=f\left(x \right)$ có bao nhiêu đường tiệm cận?

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như sau:

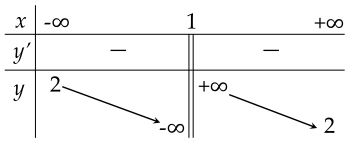
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số $y=f(x)$?

Cho hàm số $y=f(x )$ có đồ thị như hình vẽ:

Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng