Chứng minh hệ thức, trung điểm, tỉ lệ cạnh liên quan đến tứ giác nội tiếp đường tròn SVIP

Hướng dẫn giải:

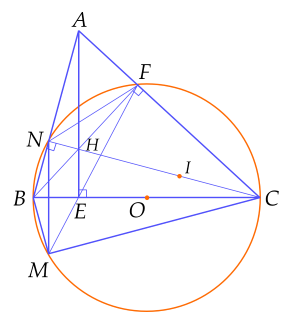
a) Gọi $I$ là trung điểm $HC$.

$HF \bot AC$ (gt) suy ra $\widehat{HFC}=90^\circ$

Xét tam giác $HFC$ vuông tại $F$, $FI$ là trung tuyến ứng với cạnh huyền nên $FI=HI=CI=\dfrac12HC$ (1)

$HE \bot BC$ (gt) suy ra $\widehat{HEC}=90^\circ$

Xét tam giác $HEC$ vuông tại $E$, $EI$ là trung tuyến ứng với cạnh huyền nên $EI=HI=CI=\dfrac12HC$ (2)

Từ (1) và (2) suy ra $FI=EI=HI=CI$.

$\Rightarrow CEHF$ là tứ giác nội tiếp đường tròn tâm $I$ đường kính $HC.$

b) $HN\bot AB$ (gt) suy ra $\widehat{ANH}=90^\circ $

$HF\bot AC$ (gt) suy ra $\widehat{AFH}=90^\circ $

Tương tự câu a) suy ra $AFHN$ là tứ giác nội tiếp.

Suy ra $\widehat{NAH}=\widehat{NFH}$ (hai góc nội tiếp cùng chắn cung $HN$) (3)

Tứ giác $HECF$ nội tiếp (cmt)

Suy ra $\widehat{HFE}=\widehat{HCE}$ (hai góc nội tiếp cùng chắn cung $HE$). (4)

Ta có $\widehat{BAE}=\widehat{NCB}$ (hai góc cùng phụ với $\widehat{ABC}$)

Suy ra $\widehat{NAH}=\widehat{HCE}$ (5)

Từ (3), (4), (5) suy ra $\widehat{NFH}=\widehat{HFE}$ hay $\widehat{NFB}=\widehat{BFM}$.

Xét $(O)$ có: $\widehat{NFB}=\widehat{BFM}$:

Suy ra sđ$\overset\frown{BN}=$ sđ$\overset\frown{BM}$ (hai góc nội tiếp bằng nhau hai cung chắn bằng nhau).

Suy ra $BN=BM$ (hai cung chắn bằng nhau hai dây bằng nhau) (đpcm).

c) Xét hai tam giác vuông $FAH$ và $FBH$ ta có:

$AH=BC$ (giả thiết)

$\widehat{FAH}=\widehat{FBC}$ (vì cùng phụ với góc $\widehat{ACE}$)

Vậy $\Delta FAH=\Delta FBC$ $\Rightarrow FA=FB$

Mặt khác tam giác $AFB$ vuông có $FA=FB$ nên nó vuông cân.

Vậy $\widehat{BAC}=45^{\circ}$.

Hướng dẫn giải:

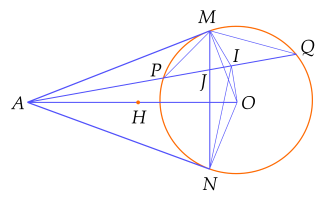
a) Gọi $H$ là trung điểm $AO$.

Xét đường tròn $(O)$ có $I$ là trung điểm của dây cung $PQ$ (dây $PQ$ không đi qua tâm $O$).

Suy ra $OI \bot PQ$ nên $\widehat{PIO}=90^\circ$

Suy ra $\widehat{AIO}=90^\circ $

Ta có $\Delta AIO$ vuông tại $I$ có trung tuyến $IH$ ứng với cạnh huyền nên $HA=HO=HI=\dfrac{1}{2}AO$ (1)

$AM$ là tiếp tuyến của $(O)$ nên $\widehat{AMO}=90^\circ $(tính chất tiếp tuyến của đường tròn)

Suy ra $\Delta AMO$ vuông tại $M$ có trung tuyến $MH$ ứng với cạnh huyền nên $HA=HO=HM=\dfrac{1}{2}AO$ (2)

Chứng minh tương tự ta có $HA=HO=HN=\dfrac{1}{2}AO$ (3)

Từ (1), (2) và (3) suy ra $HA=HO=HN=HM=HI$.

Vậy năm điểm $A,M,O,I,N$ cùng nằm trên một đường tròn đường kính $AO$.

$\widehat{JIM}=\widehat{JIN}$;

$AM, \, AN$là tiếp tuyến của đường tròn $(O)$

Suy ra $OA$ là phân giác của $\widehat{MON}$ (tính chất hai tiếp tuyến cắt nhau)

Do đó, $ \widehat{AOM}=\widehat{AON}$.

Ta có:

$\widehat{AOM}=\widehat{AIM}$ (hai góc nội tiếp cùng chắn cung $AM$)

$\widehat{AON}=\widehat{AIN}$ (hai góc nội tiếp cùng chắn cung $AN)$

Mà $\widehat{AOM}=\widehat{AON}$ (cmt)

Suy ra $\widehat{AIM}=\widehat{AIN}$ nên $\widehat{JIM}=\widehat{JIN}$ (đpcm)

b) Xét $(O)$ có: $\widehat{MQP}=\widehat{AMP}$ (cùng chắn cung $PM$)

Suy ra $\widehat{MQA}=\widehat{AMP}$

Xét $\Delta AMP$và $\Delta AQM$ có:

 $\widehat{MAQ}$ chung

 $\widehat{AMP}=\widehat{MQA}$

Vậy $\Delta AMP\backsim\Delta AQM$ (g.g)

Suy ra $\dfrac{AP}{AM}=\dfrac{AM}{AQ}$ (hai cặp cạnh tương ứng tỉ lệ)

$AP.AQ=AM^2$ (1)

Ta có: $\widehat{AMN}=\widehat{AIN}$ (cùng chắn cung $AN$) suy ra $\widehat{AMJ}=\widehat{JIN}$

Mà $\widehat{JIM}=\widehat{JIN}$ (cmt) suy ra $\widehat{AMJ}=\widehat{JIM}$

$\widehat{AMJ}=\widehat{AIM}$

Xét $\Delta AMJ$và $\Delta AIM$có:

$\widehat{MAI}$ chung

$\widehat{AMJ}=\widehat{AIM}$

Vậy $\Delta AMJ\backsim \Delta AIM$ (g.g)

Suy ra $ \dfrac{AM}{AI}=\dfrac{AJ}{AM}$ (cặp cạnh tương ứng tỉ lệ) nên $AI.AJ=AM^2$ (2)

Từ (1) và (2) suy ra $AP.AQ=AI.AJ$ (đpcm).

Hướng dẫn giải:

a) Gọi $I$ là trung điểm $EB$.

$CD$ vuông góc với $AB$ tại $F$ nên tam giác $EFB$ vuông tại $F$ có trung tuyến $FI$ ứng với cạnh huyền

Suy ra $FI=EI=BI=\dfrac{1}{2}EB$ (1)

$\widehat{AMB}=90^\circ$ do $M$ thuộc đường tròn đường kính $AB.$

Suy ra tam giác $EMB$ vuông tại $M$ có trung tuyến $MI$ ứng với cạnh huyền

Suy ra $MI=EI=BI=\dfrac{1}{2}EB$ (2)

Từ (1) và (2) suy ra $MI=EI=BI=FI$

Vậy tứ giác $BMEF$ nội tiếp đường tròn tâm $I$ đường kính $BE$.

b) Ta có $AB\bot CD\Rightarrow F$ là trung điểm của $CD$ (mối liên hệ giữa đường kính và dây cung)

Suy ra $ AB$ là đường trung trực của $CD$

Suy ra sđ$\overset\frown{AC}$ = sđ$\overset\frown{AD\,}$

Ta có $\widehat{AMC}=\dfrac{1}{2}$sđ$\overset\frown{AC}$ và $\widehat{AMD}=\dfrac{1}{2}$sđ$\overset\frown{AD}$

Do đó, $\widehat{AMC}=\widehat{AMD}\Rightarrow AM$ là phân giác của $\widehat{CMD}$

c) Xét $\Delta ACE$ và $\Delta AMC$ có: $\widehat{A}$ chung

$\widehat{AMC}=\dfrac{1}{2}$sđ$\overset\frown{AC}$ và $\widehat{ACD}=\dfrac{1}{2}$sđ$\overset\frown{AD}$

Suy ra $\widehat{AMC}=\widehat{ACD}$

Do đó, $ \Delta ACE \backsim \Delta AMC$ (g-g)

Nên $\dfrac{AC}{AM}=\dfrac{AE}{AC}$ hay $AC^2=AE.AM$

Hướng dẫn giải:

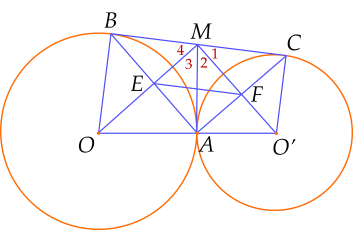
a) Chứng minh $OM$ vuông góc với $O'M$.

Vì $MA$ và $MB$ là tiếp tuyến của $(O)$ nên $MO$ là tia phân giác của $\widehat{AMB}$.

Do đó $\widehat{OMA}=\dfrac{1}{2}\widehat{BMA}$

$MA$ và $MC$ là tiếp tuyến của $\left(O' \right)$ nên $MO'$ là tia phân giác của $\widehat{AMC}$.

Do đó $\widehat{O'MA}=\dfrac{1}{2}\widehat{CMA}$

Suy ra $\widehat{OMO'}=\widehat{OMA}+\widehat{O'MA}=\dfrac12\left(\widehat{BMA}+\widehat{CMA} \right)=\dfrac{1}{2}.180^\circ=90^\circ$

Suy ra $OM \bot O'M$

b) Ta có: $MB=MA$ (tính chất của hai tiếp tuyến cắt nhau)

$OB=OA$ (bằng bán kính $R$)

Suy ra $ MO$ là đường trung trực của $AB$

Suy ra $MO\bot AB$ tại $E$ nên $ \widehat{MEA}=90^\circ$

Tương tự, ta có: $\widehat{MFA}=90^\circ$

Xét tứ giác $MEAF$ có: $\widehat{MEA}=\widehat{MFE}=\widehat{OMO'}=90^\circ$

Suy ra tứ giác $MEAF$là hình chữ nhật (theo dấu hiệu nhận biết)

Do đó $MEAF$ là tứ giác nội tiếp

Suy ra $\widehat{MFE}=\widehat{MAE}$

Trong tam giác vuông $AOM$, ta có $\widehat{MAE}=\widehat{OAE}$

Vì vậy $\widehat{MFE}=\widehat{EOO'}$.

c) Cần xác định tâm $I$ của đường tròn ngoại tiếp tứ giác $OEFO'$

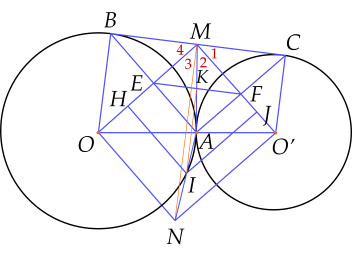
Vẽ hai đường trung trực của hai đoạn thẳng $EO$ và $FO'$ lần lượt cắt $EO$ và $FO'$ tại $H$ và $J$.

Hai đường trung trực này cắt nhau tại $I$. $I$ chính là tâm đường tròn ngoại tiếp tứ giác $OEFO'$.

Qua $O$ vẽ đường thẳng song song với $MO'$. Qua $O'$ vẽ đường thẳng song song với $MO$.

Hai đường thẳng này cắt nhau tại $N$.

Theo cách vẽ ta được tứ giác $MONO'$ là hình chữ nhật (vì có 3 góc vuông).

Suy ra $OO'=MN$ (hai đường chéo của hình chữ nhật)

Chứng minh $I$ là trung điểm của $ AN$:

Hình thang $AEON$ có $HE=HO$ và $HI$ // $EA$ // $ON$

Suy ra $HI$ đi qua trung điểm của $AN$ (1)

Tương tự, ta có $JI$ đi qua trung điểm của $AN$ (2)

Mà $I=HI \cap JI$ (3)

Từ (1), (2) và (3) suy ra $I$ là trung điểm của $AN$

Xét $\Delta AMN$có $IK$ là đường trung bình của tam giác nên

$ IK=\dfrac{1}{2}MN$ hay $ IK=\dfrac{1}{2}OO'$.

Hướng dẫn giải:

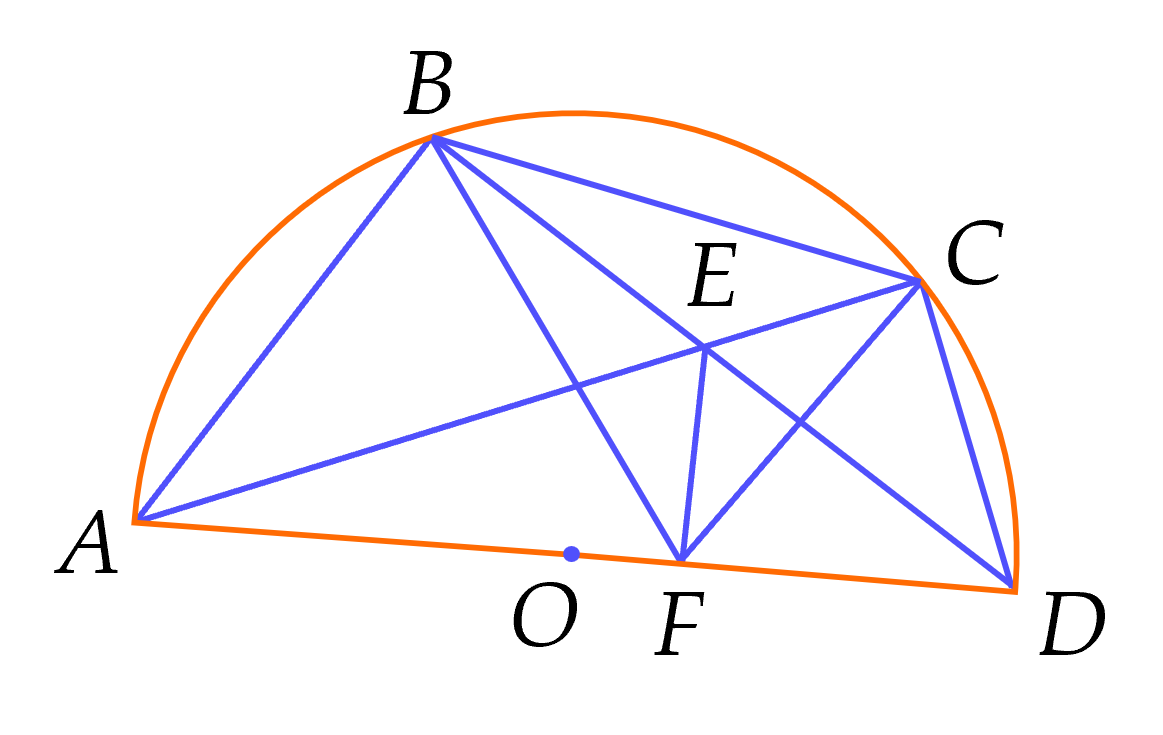
a) Chứng minh tứ giác $ABEF$nội tiếp

Gọi $I$ là trung điểm của $AE$.

$B$ thuộc $(O)$ nên $\widehat{ABD}=90^\circ $(góc nội tiếp chắn nửa đường tròn)$

Suy ra $ \widehat{ABE}=90^\circ$.

Xét tam giác $ABE$ vuông tại $B$, $BI$ là trung tuyến ứng với cạnh huyền nên $BI=EI=AI=\dfrac{1}{2}AE$ (1)

$EF\bot AD$ (gt) nên $\widehat{AFE}=90^\circ $

Xét tam giác $AFE$ vuông tại $F$, $FI$ là trung tuyến ứng với cạnh huyền nên $FI=EI=AI=\dfrac{1}{2}AE$ (2)

Từ (1) và (2) suy ra $FI=EI=AI=BI$

Suy ra $ABEF$ là tứ giác nội tiếp.

b) $C \in (O)$ suy ra $\widehat{ACD}=90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Xét $\Delta AFE$ và $\Delta ACD$ có:

$\widehat{CAD}$ chung

$\widehat{AFE}=\widehat{ACD}=90^\circ $

Do đó $\Delta AFE\backsim\Delta ACD$ (g.g)

Suy ra $\dfrac{AF}{AC}=\dfrac{AE}{AD}\Rightarrow AC.AE=AF.AD$

a) Ta chứng minh $FE$ là phân giác của $\widehat{BFC}$

Xét $\left(O \right): \, \widehat{BAC}=\widehat{BDC}$ (hai góc nội tiếp cùng chắn cung $BC$)

Suy ra $\widehat{BAE}=\widehat{EDC}\,\,(1)$

Tứ giác $ABEF$ nội tiếp (cmt) nên $\widehat{BAE}\,=\widehat{BFE}$ (cùng chắn cung $BE)$ $(2 )$

Tứ giác $CDFE$ có $\widehat{ECD}=\widehat{EFD}=90^\circ$ nên $CDFE$là tứ giác nội tiếp

Suy ra $\widehat{EFC}\,=\widehat{EDC}\,$(cùng chắn cung $EC$) (3)

Từ (1), (2), (3) ta có $\widehat{BFE}=\widehat{EFC}$ nên $FE$là phân giác của $\widehat{BFC}\,$

Chứng minh $CE$ là phân giác của góc $BCF$

Xét $\left(O \right)$có $\widehat{ACB}\,=\widehat{ADB}\,$ (cùng chắn cung $AB$)

Suy ra $\widehat{ECB}\,=\widehat{EDF}\,$

Tứ giác $CDFE$ nội tiếp (cmt) nên $\widehat{ECF}\,=\widehat{EDF}\,$ (cùng chắn cung $EF$)

Suy ra $\widehat{ECB}\,=\widehat{ECF}$ nên $CE$ là phân giác $\widehat{BCF}\,$

$\Delta BCF$ có $FE, \, CE$là hai đường phân giác cắt nhau tại $E$

Nên $E$ là tâm đường tròn nội tiếp tam giác $BCF$.

Hướng dẫn giải:

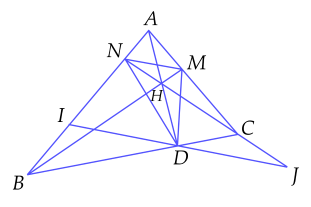
a) Ta có $HM\bot AC$ và $HN\bot AB$ suy ra $\widehat{HMA}\,=\widehat{HNA}\,=90^\circ $

Gọi $O$ là trung điểm của $AH$.

Xét tam giác $ANH$ vuông tại $N$, $NO$ là trung tuyến ứng với cạnh huyền nên $NO=AO=OH=\dfrac{1}{2}AH$ (1)

Xét tam giác $AMH$ vuông tại $M$, $MO$ là trung tuyến ứng với cạnh huyền nên $MO=AO=OH=\dfrac{1}{2}AH$ (2)

Từ (1) và (2) suy ra $MO=AO=OH=NO$

Suy ra tứ giác $AMHN$ là tứ giác nội tiếp.

b) Tương tự câu a, ta có

$\widehat{HMC}\,=\widehat{HDM}\,=90^\circ$ suy ra $HDCM$ là tứ giác nội tiếp

Suy ra $\widehat{HDM}\,=\widehat{HCM}$ (cùng chắn cung $HM$)

$\widehat{HDB}=\widehat{HNB}=90^\circ$ suy ra $HDBN$ là tứ giác nội tiếp

Suy ra $ \widehat{NDH}\,=\widehat{NBH}\,$(cùng chắn cung $HN)$

Mà $\widehat{HCM}\,=\widehat{NBH}\,$(cùng phụ với $\widehat{BAC}\,)$

Suy ra $ \widehat{HDM}=\widehat{HDN}$

Do đó, $AD $ là phân giác của $\widehat{MDN}$.

c) Ta có: Tứ giác $AMHN$ nội tiếp (cmt) suy ra $ \widehat{HNM}\,=\widehat{HAM}\,$ (cùng chắn cung $HM)$

Mà $\widehat{HAM}\,=\widehat{HBD}\,$ (cùng phụ với $\widehat{ACB}\,)$

Tứ giác $HDBN$nội tiếp suy ra $ \widehat{HBD}\,=\widehat{HND}\,$ (cùng chắn cung $HD)$

Do đó, $\widehat{HNM}\,=\widehat{HND}\,$

Ta lại có $IJ$ // $MN$ (gt) suy ra $ \widehat{HNM}\,=\widehat{HJI}\,=\widehat{HJD}\,$ (hai góc so le trong bằng nhau)

Suy ra $ \widehat{HND}\,=\widehat{HJD}\,$ hay $\Delta DNJ$ cân tại $D$ nên $DN=DJ$ $\left(1 \right)$

Vì $\widehat{HND}\,=\widehat{HJD}$ (cmt)

$90^\circ -\widehat{HND}=90^\circ -\widehat{HJD}$

$\widehat{DNI}\,=\widehat{NID}$.

Suy ra $\Delta NID$ cân tại $D$ nên $DN=DI$ (2)

Từ (1) và (2) suy ra $DI=DJ$ $(=DN)$

Vậy $D$ là trung điểm $IJ$.

Hướng dẫn giải:

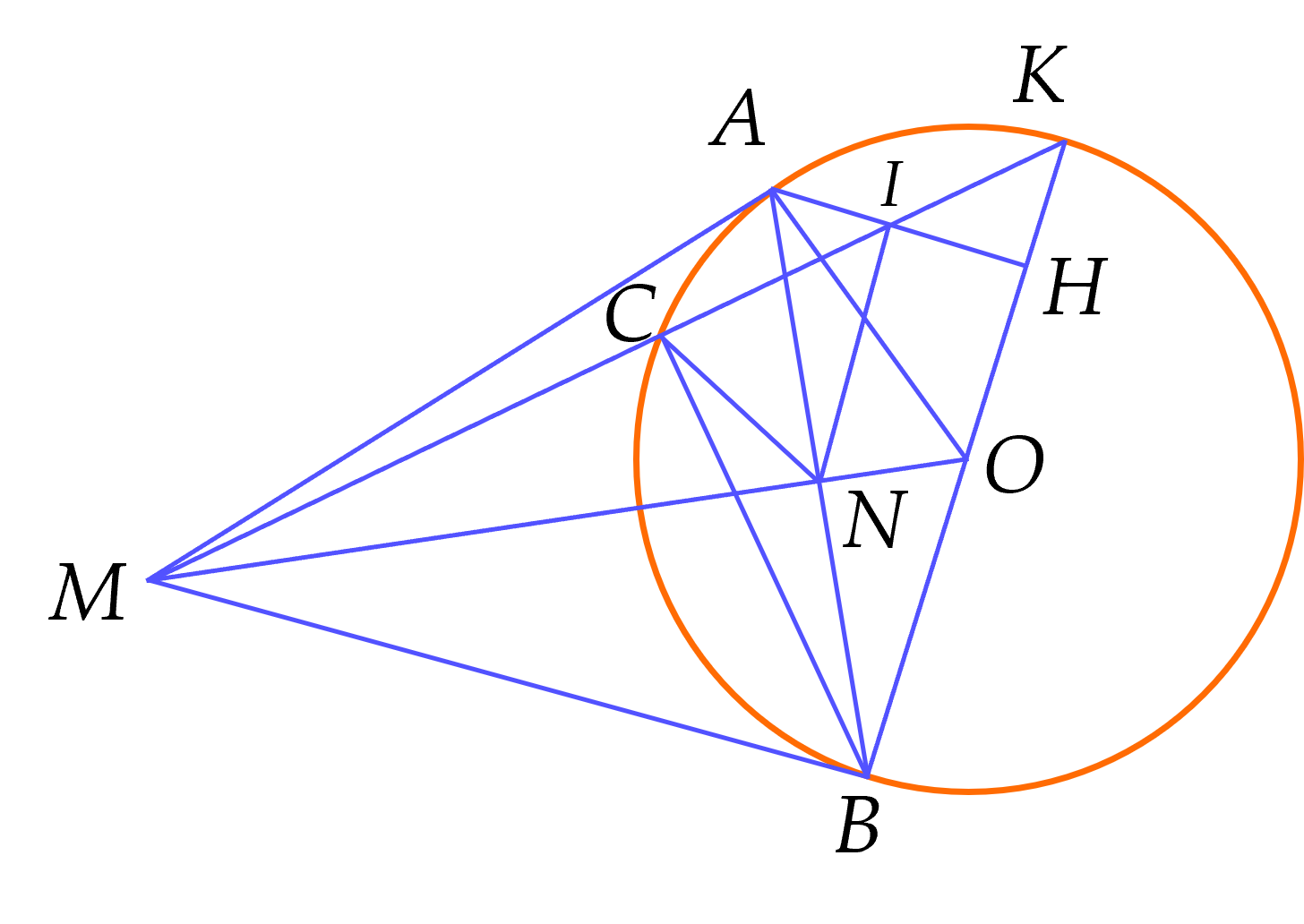
a) Vì $MA, \, MB$ là các tiếp tuyến của $(O)$ lần lượt tại $A, \, B$ nên $\widehat{MAO}=\widehat{MBO}=90^\circ $ (định nghĩa).

Gọi $P$ là trung điểm của $OM$.

Xét tam giác $MAO$ vuông tại $A$, $AP$ là trung tuyến ứng với cạnh huyền nên $AP=PO=PM=\dfrac{1}{2}OM$ (1)

Xét tam giác $MBO$ vuông tại $B$, $BP$ là trung tuyến ứng với cạnh huyền nên $BP=PO=PM=\dfrac{1}{2}OM$ (2)

Từ (1) và (2) suy ra $BP=PO=PM=AP$

Suy ra tứ giác $MAOB$ nội tiếp đường tròn tâm $P$ đường kính $OM$.

b) Gọi $N$ là giao điểm của $AB$ với $MO$.

$C$ là giao điểm giữa $MK$ với đường tròn $(O)$

Ta có: $OA=OB$ suy ra $O$ thuộc trung trực của $AB$.

Tứ giác $MCNB$ có $\widehat{MCB}=\widehat{MNB}=90^\circ $.

Suy ra tứ giác $MCNB$ nội tiếp.

Khi đó $\widehat{NMB}=\widehat{NCB}$ (hai góc cùng chắn một cung $BN$)

Ta có: $\widehat{NMB}=\widehat{NBO}$ (cùng phụ với $\widehat{MBN}$)

Suy ra $ \widehat{NCB}=\widehat{NBO}.$

Mà $\widehat{NCB}+\widehat{NCI}=90^\circ, \, \widehat{NAI}+\widehat{NBO}=90^\circ $

Suy ra $\widehat{NCI}=\widehat{NAI}$.

Xét tứ giác $ACNI$ có: $\widehat{NCI}=\widehat{NAI}$ (cmt), suy ra tứ giác $ACNI$ nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).

$\Rightarrow \widehat{ANI}=\widehat{ACI}$ (hai góc cùng chắn cung $AI$).

Trong $(O)$ có: $\widehat{ACI}=\widehat{ABK}$ (hai góc nội tiếp cùng chấn cung $AK$)

Suy ra $\widehat{ANI}=\widehat{ABK}$.

Mà hai góc này vị trí đồng vị nên $NI$ // $BK$

Tam giác $ABK$ có: $NI$ // $BK$ và $NA=NB=\dfrac{1}{2}AB$

Suy ra $I$ là trung điểm của $AH$ nên $IA=IH$ (định lí đường trung bình của tam giác) (đpcm).

Hướng dẫn giải:

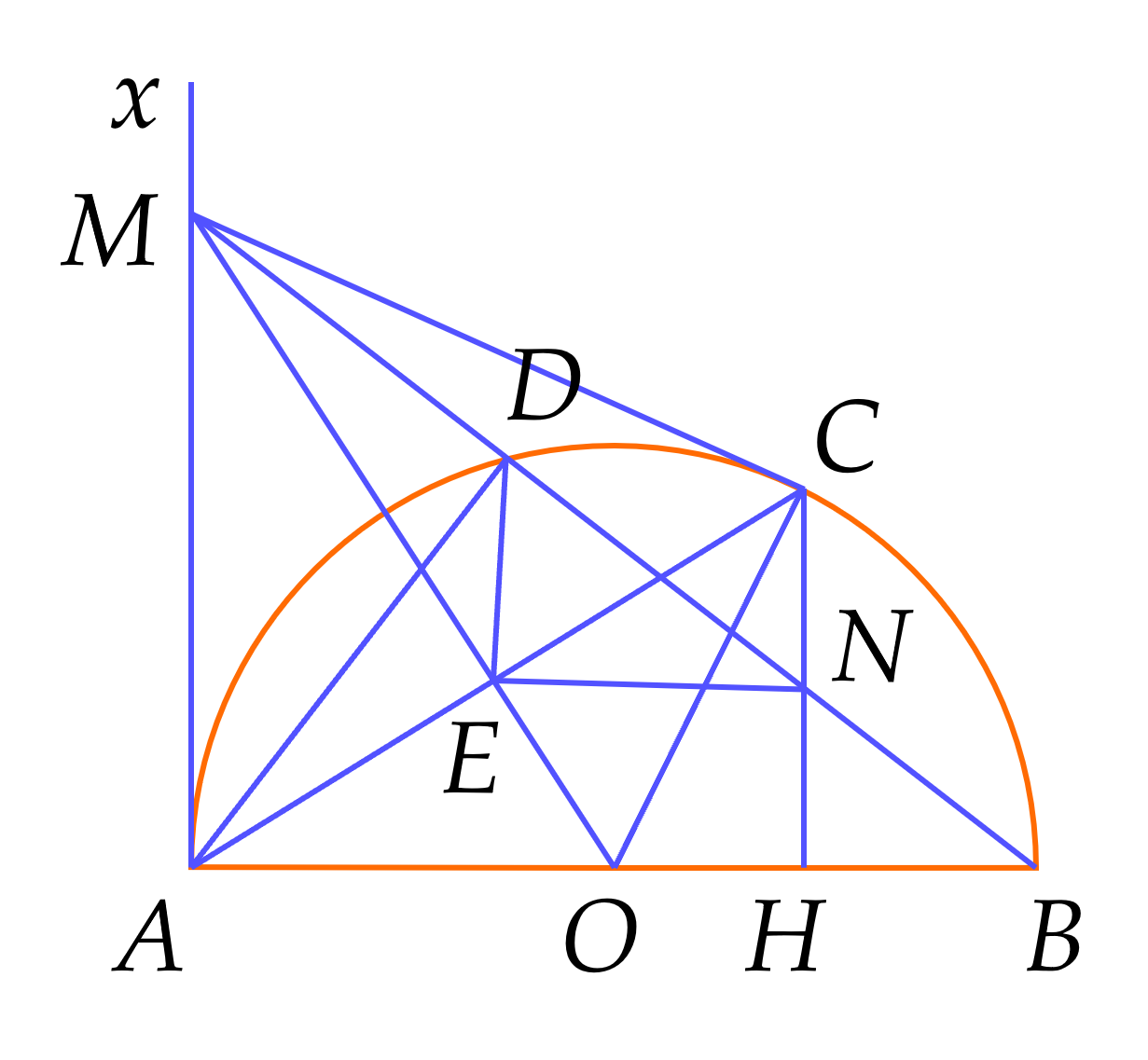
a) Ta có: $OA=OC$ nên $O$ thuộc trung trực của $AC$.

$MA=MC$ (tính chất hai tiếp tuyến cắt nhau) nên $M$ thuộc trung trực của $AC$.

Suy ra $OM$ là trung trực của $AC$ hay $OM\bot AC$ tại $E$

Do đó, $\widehat{AEM}=90^\circ $.

Ta có $\widehat{ADB}=90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Hay $\widehat{ADM}=90^\circ $.

Gọi $I$ là trung điểm $AM$.

Xét tam giác $MAD$ vuông tại $D$, $DI$ là trung tuyến ứng với cạnh huyền nên $DI=MI=AI=\dfrac{1}{2}AM$ (1)

Xét tam giác $MAE$ vuông tại $E$, $EI$ là trung tuyến ứng với cạnh huyền nên $EI=MI=AI=\dfrac{1}{2}AM$ (2)

Từ (1) và (2) suy ra $DI=EI=MI=AI$

Suy ra $AMDE$ là tứ giác nội tiếp đường tròn đường kính $AM$.

b) Xét $\Delta MAD$ và $\Delta MBA$ có:

$\widehat{AMB}$ chung;

$\widehat{MDA}=\widehat{MAB}=90^\circ $

Do đó, $ \Delta MAD\backsim\Delta MBA$ (g.g)

Suy ra $ \dfrac{MA}{MD}=\dfrac{MB}{MA}$ (hai cạnh tương ứng)

Suy ra $MA^2=MD.MB$.

c) Gọi $MB\cap CH=\{N\}$.

Vì $AEDM$ là tứ giác nội tiếp (cmt) nên $\widehat{DEC}=\widehat{AMD}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).

Mà $\widehat{AMD}=\widehat{DAB}$ (cùng phụ với $\widehat{MAD}$) nên $\widehat{DEC}=\widehat{DAB}$ (1).

Ta có $\widehat{DNC}=\widehat{BNH}$ (đối đinh), mà $\widehat{BNH}+\widehat{NBH}=90^\circ$

$\widehat{DAB}+\widehat{NBH}=90^\circ$

Suy ra $ \widehat{BNH}=\widehat{DAB}$ hay $\widehat{DNC}=\widehat{DAB}$ (2).

Từ (1) và (2) suy ra $\widehat{DEC}=\widehat{DNC}$.

Do đó, $DENC$ là tứ giác nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).

Suy ra $\widehat{DNE}=\widehat{DCE}$ (hai góc nội tiếp cùng chắn cung $DE$).

Mà $\widehat{DCE}=\widehat{DCA}=\widehat{DBA}$ (hai góc nội tiếp cùng chắn cung $DA$).

Suy ra $ \widehat{DNE}=\widehat{DBA}$.

Mà hai góc này nằm ở vị trí đồng vị nên $EN$ // $AB$ hay $EN$ // $AH$.

Mà $E$ là trung điểm của $AC$ (do $OM$ là trung trực của $AC,OM\cap AC=\{E\}$).

Nên $N$ là trung điểm của $CH$ (định lí đường trung bình trong tam giác $ACH$).

Vậy $MB$ đi qua $N$ là trung điểm của $CH$ (đpcm).

Hướng dẫn giải:

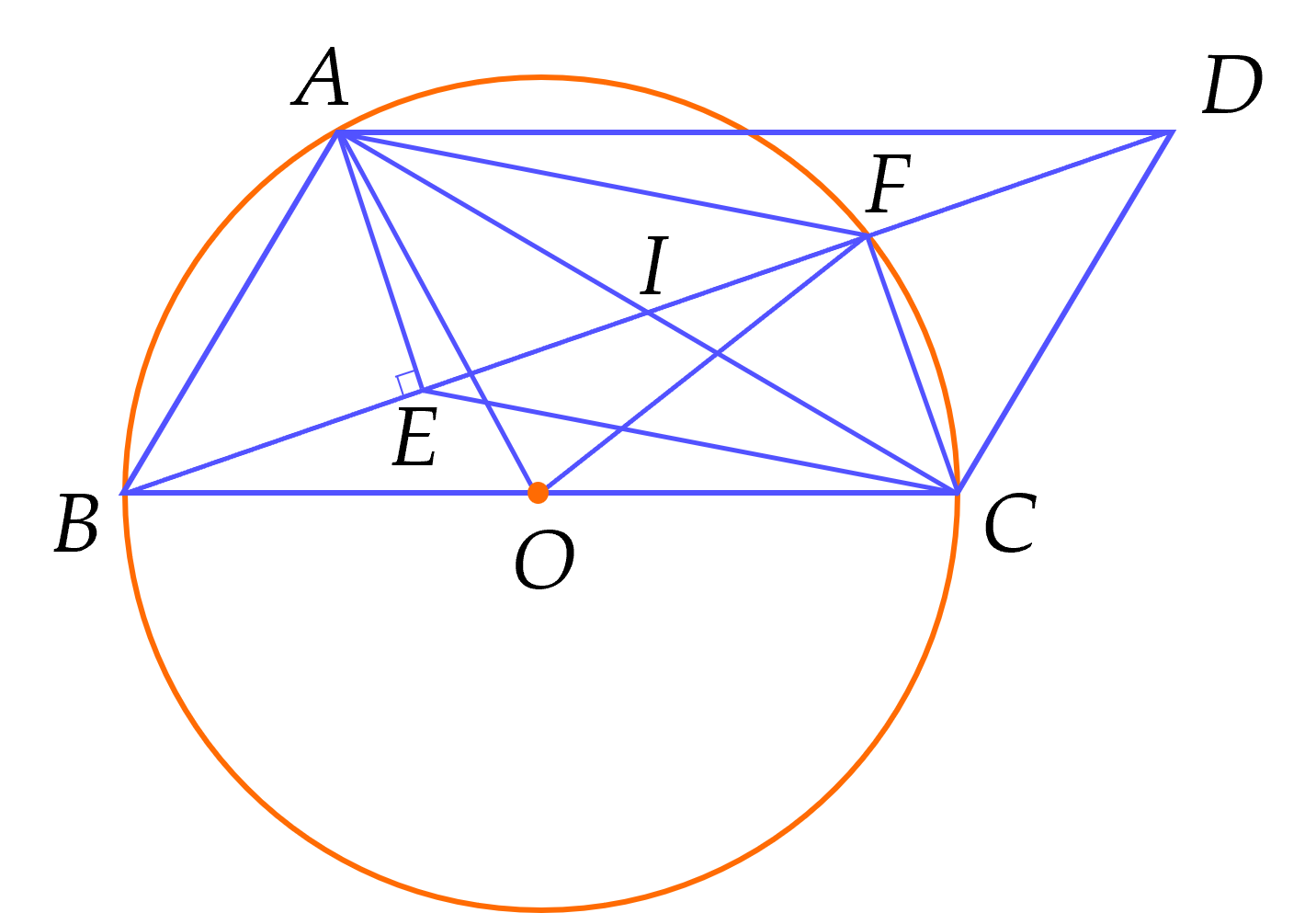
a) ta có $\widehat{BAC}=90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Tứ giác $ABCD$ là hình bình hành suy ra $AB$ // $CD$ nên $\widehat{ACD}=\widehat{BAC}=90^\circ $ (hai góc so le trong)

Gọi $N$ là trung điểm của $AD$.

Xét tam giác $DAE$ vuông tại $E$, $EN$ là trung tuyến ứng với cạnh huyền nên $EN=AN=ND=\dfrac{1}{2}AD$ (1)

Xét tam giác $DAC$ vuông tại $C$, $CN$ là trung tuyến ứng với cạnh huyền nên $CN=AN=ND=\dfrac{1}{2}AD$ (2)

Từ (1) và (2) suy ra $EN=CN=AN=ND$

Do đó tứ giác $AECD$ nội tiếp.

b) Tứ giác $AECD$ nội tiếp suy ra $ \widehat{CAE}=\widehat{CDE}$ (hai góc nội tiếp chắn cung $EC$)

$AB$ // $CD$ suy ra $ \widehat{CDE}=\widehat{ABD}$ (so le trong)

Suy ra $\widehat{CAE}=\widehat{ABD}$

Mà $\widehat{ABD}$ là góc ở tâm; $\widehat{AOF}$ là góc nội tiếp chắn cung $AF$

Nên $\widehat{AOF}=2.\widehat{ABD}$ hay $\widehat{AOF}=2.\widehat{CAE}$

c) Ta có $\widehat{BFC}=90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Suy ra $AE$ // $CF$ (cùng vuông góc với $BD$)

Lại có $\widehat{AFB}=\widehat{ACB}=\widehat{CAD}=\widehat{FEC}$ nên $AF$ // $EC$

Do đó tứ giác $AECF$ là hình bình hành.

d) Gọi giao điểm của $AC$ và $BD$blà $I$, do tứ giác $ABCD$ là hình bình hành nên $IA=IC;IB=ID;AB=CD$

Xét tam giác $DCI$ vuông tại $C$ có $CF$ là đường cao nên $CD^2=DF.DI$ hay $AB^2=DF.DI$

Suy ra $2AB^2=2.DF.DI$ mà $2DI=BD$ do đó $2A{{B}^{2}}=DF.BD$.

Hướng dẫn giải:

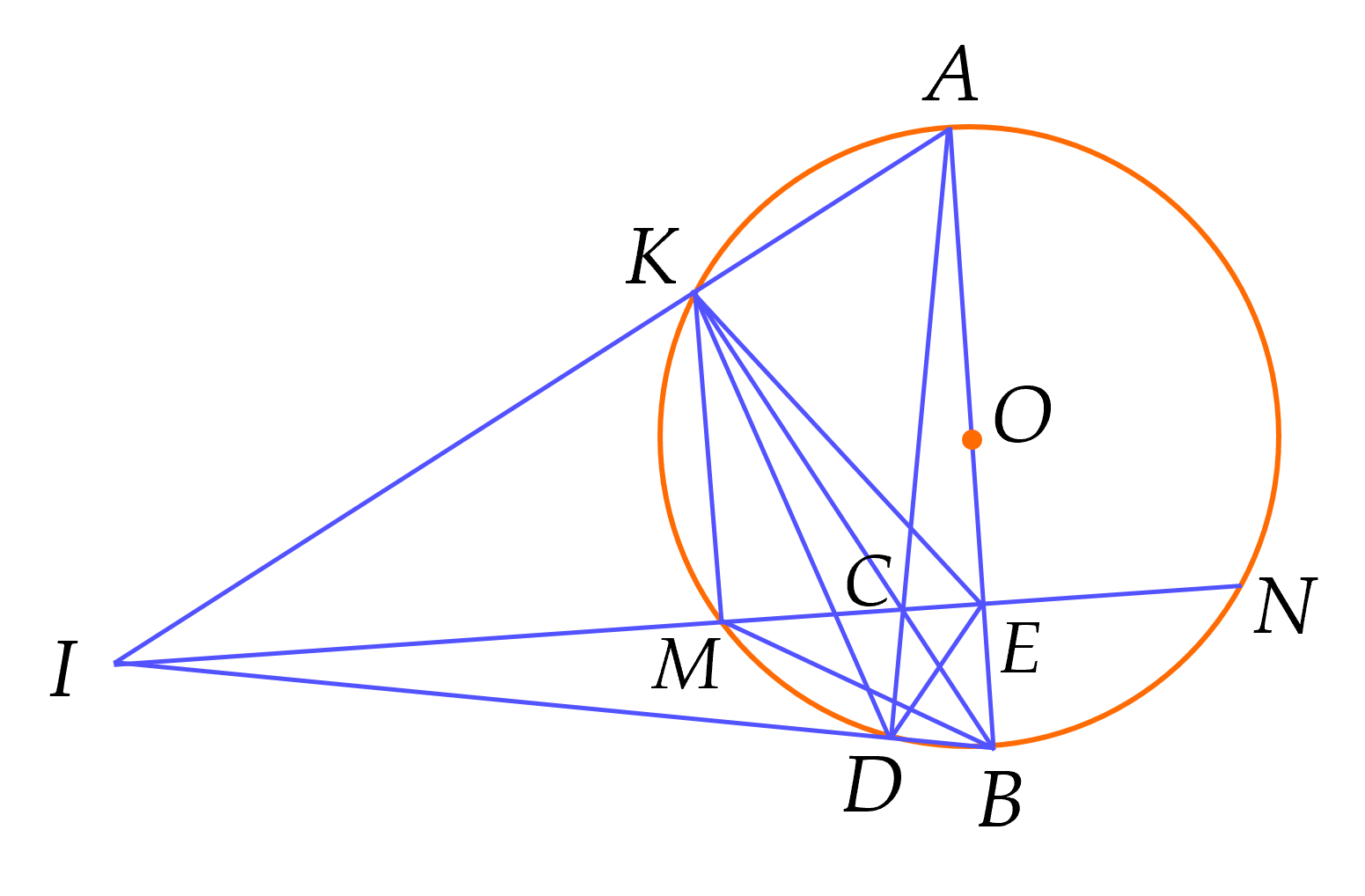
a) Ta có:$\widehat{AKE}=90^\circ $ (góc nội tiếp chắn nửa đường tròn) suy ra $\widehat{AKC}=90^\circ $

$AB\bot MN$ tại $E$ nên $\widehat{AEC}=90^\circ $

Gọi $P$ là trung điểm $AC.$

Xét tam giác $AKC$ vuông tại $K$, $KP$ là trung tuyến ứng với cạnh huyền nên $KP=AP=PC=\dfrac{1}{2}AC$ (1)

Xét tam giác $AEC$ vuông tại $E$, $EP$ là trung tuyến ứng với cạnh huyền nên $EP=AP=PC=\dfrac{1}{2}AC$ (2)

Từ (1) và (2) suy ra $EP=KP=AP=PC$

Vậy $AKCE$ là tứ giác nội tiếp.

2) Ta có $AB\bot MN$ nên $B$ là điểm chính giữa cung $MN$ suy ra sđ$\overset\frown{BM}=$ sđ$\overset\frown{BN}$

Suy ra $ \widehat{BMN}=\widehat{MKB}$ (2 góc nội tiếp chắn hai cung bằng nhau)

Suy ra $\widehat{BMC}=\widehat{BKM}$

Xét $\Delta BCM$ và $\Delta BMK$ có:

$\widehat{MBK}$ chung

$\widehat{BMC}=\widehat{BKM}$ (cmt)

Suy ra $\Delta BCM \backsim \Delta BMK$ (g.g)

Do đó, $ \dfrac{BC}{BM}=\dfrac{BM}{BK}$ hay $B{{M}^{2}}=BC. BK.$

3) Tam giác $ABI$ có $BK\bot AI$ (do $\widehat{AKB}=90^\circ$),

$IE\bot AB$ (do $AB\bot MN$)

Do đó, $BK,IE$ là hai đường cao của $\Delta ABI$ nên $C$ là trực tâm $\Delta ABI$

Suy ra $AD$ là đường cao của tam giác $ABI$ suy ra $ AD\bot IB$

Hay $\widehat{ADB}=90{}^\circ $

Mà $AB$vlà đường kính của đường tròn $\left(O \right)$ suy ra $D\in \left(O \right)$

Xét $\left(O \right)$ có:

$\widehat{ADK}=\widehat{ABK}$ (hai góc nội tiếp cùng chắn cung $AK)$

$\widehat{DKB}=\widehat{DAB}$ (hai góc nội tiếp cùng chắn cung $BD)$

Tứ giác $AKCE$ nội tiếp suy ra $ \widehat{CKE}=\widehat{CAE}$ (hai góc nội tiếp cùng chắn cung $CE)$

$ \widehat{BKE}=\widehat{DAB}$

$\widehat{DKB}=\widehat{DAB}$

Do đó, $KB$ là tia phân giác của $\widehat{DKE}$

Tứ giác $BDCE$ có: $\,\widehat{BDC}=90{}^\circ ;\widehat{CEB}=90{}^\circ $

$\Rightarrow BDCE$ là tứ giác nội tiếp

Suy ra $\widehat{CDE}=\widehat{CBE}$ (cùng chắn cung $CE)$

Suy ra $\widehat{ADE}=\widehat{ABK}$

$\widehat{ADK}=\widehat{ADE}$

$DA$ là tia phân giác của $\widehat{EDK}$

Tam giác $DEK$ có:

$KB$ là tia phân giác của $\widehat{DKE};\,DA$ là tia phân giác của $\widehat{EDK}$

Mà $C$ là giao điểm của $KB,DA$ suy ra $ C$là tâm đường tròn nội tiếp $\Delta DEK$

Vậy $C$ cách đều ba cạnh của tam giác $DEK$.

Hướng dẫn giải:

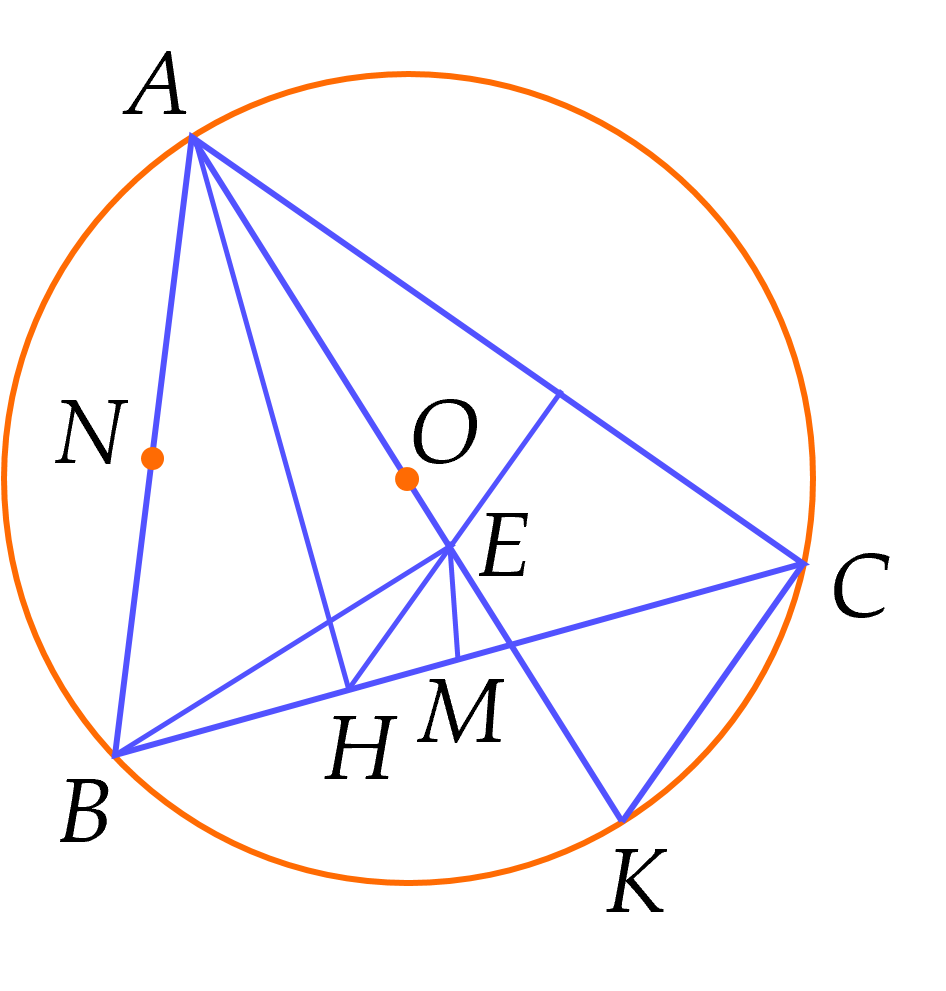
a) Chứng minh $AEHB$ là tứ giác nội tiếp

Ta có: $AH\bot BC$ nên $ \widehat{AHB}=90^\circ,$

$AE\bot BE$ nên $\widehat{AEB}=90^\circ $

Gọi $N$ là trung điểm của $AB$.

Xét tam giác $BAE$ vuông tại $E$, $EN$ là trung tuyến ứng với cạnh huyền nên $EN=AN=NB=\dfrac{1}{2}AB$ (1)

Xét tam giác $BAH$ vuông tại $H$, $HN$ là trung tuyến ứng với cạnh huyền nên $HN=AN=NB=\dfrac{1}{2}AB$ (2)

Từ (1) và (2) suy ra $EN=HN=AN=NB$ nên $AEHB$ là tứ giác nội tiếp.

b) Kéo dài $AO$ cắt đường tròn $\left(O \right)$ tại $K$ khi đó $AK$ là đường kính của đường tròn tâm $O$, ta có $C$ thuộc đường tròn $(O)$ suy ra $\widehat{ ACK}=90^\circ $ (góc nội tiếp chắn nửa đường tròn)

Do đó, $CK\bot AC$

Tứ giác $AEHB$ nội tiếp (cmt)$\Rightarrow \widehat{EHC}=\widehat{BAE}$(hai góc cùng bù với $\widehat{EHB})$

$\Rightarrow \widehat{EHC}=\widehat{KAB}$

Xét (O) có: $\widehat{KAB}=\widehat{BCK}$ (hai góc nội tiếp cùng chắn cung BK)

$\Rightarrow \widehat{EHC}=\widehat{BCK}$mà hai góc này ở vị trí so le trong $\Rightarrow HE//CK$

Ta có $C K\bot AC$ (cmt)

$CK$ // $HE$

Suy ra $HE\bot AC$

c) Ta có $N$ là tâm đường tròn ngoại tiếp tứ giác $ABHE$ suy ra $NE=NH$ (1)

Tam giác $ABC$có: M, N lần lượt là trung điểm $BC,AB$

Suy ra $MN$là đường trung bình của tam giác $ABC\Rightarrow MN//AC$

Mà $HE\bot AC(cmt)\Rightarrow MN\bot HE\left(2 \right)$

Từ (1) và $\left(2 \right)\Rightarrow MN$là đường trung trực của $HE\Rightarrow MH=ME\Rightarrow \dfrac{ME}{MH}=1$.