Bài học cùng chủ đề
- Một số dấu hiệu nhận biết tứ giác nội tiếp
- Chứng minh tứ giác nội tiếp (Phần 1)
- Chứng minh tứ giác nội tiếp (Phần 2)
- Tứ giác nội tiếp
- Tứ giác nội tiếp
- Phương pháp: Chứng minh tổng hai góc đối bằng 180 độ
- Phương pháp: Chứng minh hai đỉnh kề nhau cùng nhìn cạnh chứa hai điểm còn lại hai góc bằng nhau
- Phương pháp: Chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
- Chứng minh đẳng thức tích các đoạn thẳng
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Chứng minh đẳng thức tích các đoạn thẳng SVIP
Cho đường tròn tâm $(O)$, bán kính $R$. Từ một điểm $M$ ở ngoài đường tròn, kẻ hai tiếp tuyến $MA$ và $MB$ với đường tròn ($A$, $B$ là các tiếp điểm). Qua $A$ kẻ đường thẳng song song với $MO$ cắt đường tròn tại $E$ ($E$ khác $A$), đường thẳng $ME$ cắt đường tròn tại $F$ ($F$ khác $E$). Đường thẳng $AF$ cắt $MO$ tại $N$, $H$ là giao điểm của $MO$ và $AB$.
a) Chứng minh tứ giác $MAOB$ nội tiếp đường tròn.
b) Chứng minh $MN^2 = NF.NA$ và $MN = NH$.
Hướng dẫn giải:

a) Do MA, MB là các tiếp tuyến nên \(\widehat{MAO}=\widehat{MBO}=90^o\).
Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^o\) nên MAOB là tứ giác nội tiếp.
b) Ta có do AE//MO nên \(\widehat{AEM}=\widehat{FMN}\) (So le trong)
Lại có \(\widehat{AEM}=\widehat{MAN}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn các cung bằng nhau)
Vậy nên \(\widehat{MAN}=\widehat{FMN}\).
Suy ra \(\Delta AMN\sim\Delta MFN\left(g-g\right)\)
\(\Rightarrow\dfrac{MN}{FN}=\dfrac{AN}{MN}\Rightarrow MN^2=NA.NF.\)
Tương tự ta cũng có:
\(\Delta FNH\sim\Delta HNA\left(g-g\right)\)
\(\Rightarrow\dfrac{FN}{HN}=\dfrac{NH}{NA}\Rightarrow HN^2=NA.NF.\)
Vậy nên MN2 = HN2 hay MN = NH.
Cho đường tròn $(O)$ ngoại tiếp tam giác nhọn $ABC$. Gọi $M$ và $N$ lần lượt là điểm chính giữa cung nhỏ $AB$ và cung nhỏ $BC$. Hai dây $AN$ và $CM$ cắt nhau tại điểm $I$. Dây $MN$ cắt các cạnh $AB$ và $BC$ lần lượt tại các điểm $H$ và $K$.
1) Chứng minh $C$, $N$, $I$, $K$ cùng thuộc một đường tròn.
2) Chứng minh $NB^2 = NK.NM$.
Hướng dẫn giải:
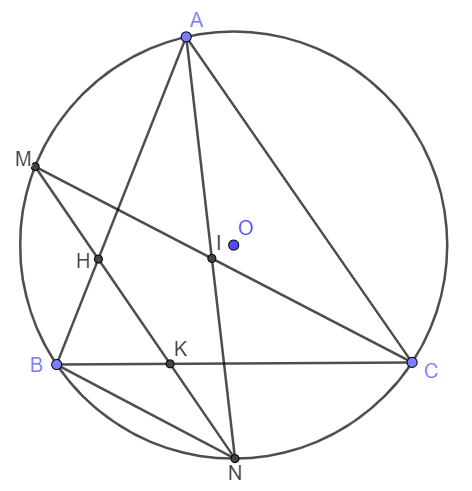
a) Do M là điểm chính giữa cung AB nên \(\stackrel\frown{AM}=\stackrel\frown{MB}\) .
Suy ra \(\widehat{ACM}=\widehat{MCB}\) (Hai góc nội tiếp chắn các cung bằng nhau)
Lại có \(\widehat{ACM}=\widehat{ANM}\) (Hai góc nội tiếp cùng chắn một cung)
Nên \(\widehat{INK}=\widehat{ICK}\)
Xét tứ giác KICN có \(\widehat{INK}=\widehat{ICK}\) nên KICN là tứ giác nội tiếp hay C, N, K, I cùng thuộc một đường tròn.
b) Do N là điểm chính giữa cung BC nên \(\stackrel\frown{BN}=\stackrel\frown{NC}\)
Vậy thì \(\widehat{BMN}=\widehat{KBN}\) (Hai góc nội tiếp chắn các cung bằng nhau)
Xét tam giác BMN và tam giác KBN có:
Góc B chung
\(\widehat{BMN}=\widehat{KBN}\)
\(\Rightarrow\Delta BMN\sim\Delta KBN\left(g-g\right)\)
\(\Rightarrow\dfrac{BN}{KN}=\dfrac{MN}{BN}\Rightarrow NB^2=NK.NM\).
Cho tứ giác $ABCD$ nội tiếp đường tròn đường kính $AD$. Hai đường chéo $AC$ và $BD$ cắt nhau tại $E$. Gọi $F$ là điểm thuộc đường thẳng $AD$ sao cho $EF$ vuông góc với $AD$. Đường thẳng $CF$ cắt đường tròn đường kính $AD$ tại điểm thứ hai là $M$. Gọi $N$ là giao điểm của $BD$ và $CF$. Chứng minh rằng:
a) $CEFD$ nội tiếp đường tròn.
b) $FA$ là đường phân giác của góc $BFM$.
c) $BD.NE = BE.ND$.
Hướng dẫn giải:

a) Xét tứ giác CEFD có \(\widehat{ECD}+\widehat{EFD}=90^o+90^o=180^o\)
nên CEFD là tứ giác nội tiếp.
b) Do CEFD là tứ giác nội tiếp nên \(\widehat{ECF}=\widehat{EDF}\) (Hai góc nội tiếp cùng chắn cung EF)
Tương tự ta cũng có tứ giác BEFA nội tiếp và \(\widehat{EBF}=\widehat{EBF}\)
Vậy thì \(\widehat{ECF}+\widehat{EAF}=\widehat{EDF}+\widehat{EBF}\).
Mà theo tính chất góc ngoài của tam giác ta có:
\(\widehat{ECF}+\widehat{EAF}=\widehat{AFM};\widehat{EDF}+\widehat{EBF}=\widehat{AFB}\)
nên \(\widehat{AFM}=\widehat{AFB}\) hay AF là phân giác của góc BFM.
c) Do FA là phân giác góc BFM mà \(FA\perp FE\) nên FE là phân giác góc \(\widehat{BFC}\)
Xét tam giác FBN:
Theo tính chất đường phân giác trong ta có:
\(\dfrac{BE}{EN}=\dfrac{BF}{FN}\) (1)
Theo tính chất đường phân giác ngoài ta có:
\(\dfrac{BF}{FN}=\dfrac{BD}{DN}\) (2)
Từ (1) và (2) suy ra \(\dfrac{BE}{EN}=\dfrac{BD}{DN}\Rightarrow BD.NE=BE.ND\) (đpcm)
Cho tam giác $ABC$ ($AB < AC$), có ba góc nhọn nội tiếp đường tròn $(O)$ và $D$ là hình chiếu vuông góc của $B$ trên $AO$ sao cho $D$ nằm giữa $A$ và $O$. Gọi $M$ là trung điểm $BC$, $N$ là giao điểm của $BD$ và $AC$, $F$ là giao điểm của $MD$ và $AC$. $E$ là giao điểm thứ hai của $BD$ với đường tròn $(O)$, $H$ là giao điểm của $BF$ và $AD$. Chứng minh rằng:
a/ Tứ giác $BDOM$ nội tiếp và \(\widehat{MOD}+\widehat{NAE}=180^o\).
b/ $DF//CE$, từ đó suy ra $NE.NF = NC.ND$.
Hướng dẫn giải:

a/ Trong đường tròn (O), M là trung điểm của dây cung BC nên \(OM\perp BC\).
Xét tứ giác BDOM có:
\(\widehat{BDO}=90^o;\widehat{BMO}=90^o\Rightarrow\widehat{BDO}+\widehat{BMO}=180^o\) nên BDOM là tứ giác nội tiếp.
b/ Xét tam giác OBC có OB = OC nên OBC làm tam giác cân tại O.
Vậy OM là phân giác góc BOC hay \(\widehat{BOM}=\dfrac{\widehat{BOC}}{2}\).
Do tứ giác BDOM nội tiếp (cma) nên \(\widehat{BDM}=\widehat{BOM}\).
Suy ra \(\widehat{BDM}=\dfrac{\widehat{BOC}}{2}\) (1)
Xét đường tròn (O), ta có \(\widehat{BEC}=\dfrac{\widehat{BOC}}{2}\) (Góc nội tiếp và góc ở tâm cùng chắn một cung) (2)
Từ (1) và (2) suy ra \(\widehat{BDM}=\widehat{BEC}\).
Mà chúng lại ở vị trí đồng vị nên DM//CE hay DF//CE.
Do DF//CE (cmt), áp dụng định lý Ta-let ta có:
\(\dfrac{NF}{NC}=\dfrac{ND}{NE}\Rightarrow NE.NF=NC.ND\).
Cho tam giác $ABC$ có ba góc nhọn ($AB < AC$), dựng $AH$ vuông góc với $BC$ tại $H$. Gọi $M$, $N$ theo thứ tự là hình chiếu vuông góc của điểm $H$ trên $AB$ và $AC$. Đường thẳng $MN$ cắt đường thẳng $BC$ tại điểm $D$. Trên nửa mặt phẳng bờ $CD$ chứa điểm $A$ vẽ nửa đường tròn đường kính $CD$. Qua $B$ kẻ đường thẳng vuông góc với $CD$ cắt nửa đường tròn trên tại điểm $E$.
a) Chứng minh tứ giác $AMHN$ là tứ giác nội tiếp.
b) Chứng minh \(\widehat{EBM}=\widehat{DNH}\).
c) Chứng minh $DM.DN = DB.DC$.
Hướng dẫn giải:
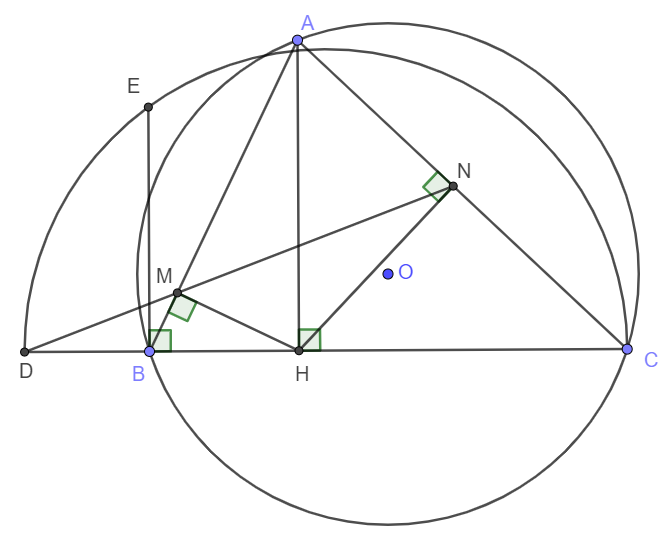
a) Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=90^o+90^o=180^o\) nên AMHN là tứ giác nội tiếp.
b) Do AMHN là tứ giác nội tiếp nên \(\widehat{MNH}=\widehat{MAH}\) (Hai góc nội tiếp cùng chắn cung MH)
Lại có AH và EB cùng vuông góc với BC nên AH//EB.
Vậy thì \(\widehat{EBM}=\widehat{MAH}\) (Hai góc so le trong)
Từ đó ta có \(\widehat{EBM}=\widehat{MNH}\).
c) Ta có \(\widehat{DMB}=\widehat{AMN}\) (Hai góc đối đỉnh)
\(\widehat{AMN}=\widehat{AHN}\) (Hai góc nội tiếp cùng chắn cung AN)
Mà \(\widehat{AHN}=\widehat{DCN}\) (Cùng phụ với góc NHC)
Nên \(\widehat{DMB}=\widehat{DCN}\).
Từ đó suy ra \(\Delta DMB\sim\Delta DCN\left(g-g\right)\)
\(\Rightarrow\dfrac{DM}{DC}=\dfrac{DB}{DN}\Rightarrow DM.DN=DB.DC\).
Cho tam giác $ABC$ có ba góc nhọn. Đường tròn $(O)$ đường kính $BC$ cắt các cạnh $AB$, $AC$ tại các điểm $D$ và $E$. Gọi $H$ là giao điểm của hai đường thẳng $BE$ và $CD$.
a) Chứng minh tứ giác $ADHE$ nội tiếp trong một đường tròn. Xác định tâm $I$ của đường tròn này.
b) Gọi $M$ là giao điểm của $AH$ và $BC$. Chứng minh $CM.CB = CE.CA$.
Hướng dẫn giải:

a) Do D, E cùng thuộc đường tròn (O) nên \(\widehat{ADH}=\widehat{AEH}=90^o\)
Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=180^o\) nên ADHE là tứ giác nội tiếp.
Gọi I là trung điểm AH, ta thấy ngay I là tâm đường tròn.
Thật vậy, theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có \(IA=ID=IB=IE\) hay I chính là tâm đường tròn.
b) Do ADHE là tứ giác nội tiếp nên \(\widehat{EAH}=\widehat{EDH}\) (Hai góc nội tiếp cùng chắn cung HE)
Lại có \(\widehat{EDH}=\widehat{EDC}=\widehat{EBC}\) (Hai góc nội tiếp cùng chắn cung EC)
Nên \(\widehat{EAH}=\widehat{HBM}\).
Xét tam giác CBE và tam giác CAM có:
\(\widehat{EAH}=\widehat{HBM}\)
Góc C chung
Vậy nên \(\Delta CBE\sim\Delta CAM\left(g-g\right)\Rightarrow\dfrac{CB}{CA}=\dfrac{CE}{CM}\)
\(\Rightarrow CM.CB=CE.CA\) (đpcm).
