Bài học cùng chủ đề
Căn bậc hai và căn thức bậc hai SVIP
O. NHẮC LẠI KIẾN THỨC
Căn bậc hai số học
Căn bậc hai số học của một số $a$ không âm là số $x$ không âm sao cho $x^2 = a$. Kí hiệu là $\sqrt a$.
Ví dụ 1. Căn bậc hai số học của $4$ là $2$ vì $2 > 0$ và $2^2 = 4$.
1. CĂN BẬC HAI
Khái niệm
Căn bậc hai của số thực $a$ không âm là số thực $x$ sao cho $x^2 = a$.
Ví dụ 2. Các căn bậc hai của:
a) $81$ là $9$ và $-9$ vì $(-9)^2 = 9^2 = 81$;
b) $0$ là $0$.
Nhận xét
▪️ Số dương $a$ có đúng hai căn bậc hai đối nhau là $\sqrt a$ (căn bậc hai số học của $a$) và $-\sqrt a$.
▪️ Số $0$ có một căn bậc hai duy nhất là $0$;
▪️ Số âm không có căn bậc hai.
Sử dụng máy tính cầm tay
Ta sử dụng máy tính cầm tay tính căn bậc hai của $a > 0$ bằng cách tính $\sqrt a$.
Ví dụ 3. Sử dụng MTCT, tính căn bậc hai của $\dfrac7{11}$ (làm tròn kết quả đến chữ số thập phân thứ nhất).
Lời giải
Bấm các phím s7a11=
Ta có kết quả: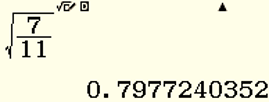 
Vậy các căn bậc hai của $\dfrac7{11}$ là $0,8$ và $-0,8$.
Tính chất
Với mọi số thực $a$ ta có $\sqrt{a^2} = |a|$.
Ví dụ 4. Tính (không sử dụng MTCT): $P = \sqrt{(-3)^2} + 3$.
Lời giải
Ta có $\sqrt{(-3)^2} = |-3| = 3$.
Vậy $P = 3+3 = 6$.
2. CĂN THỨC BẬC HAI
Định nghĩa
Căn thức bậc hai là biểu thức có dạng $\sqrt A$, trong đó $A$ là một biểu thức đại số.
$A$ được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn.
Điều kiện xác định
$A$ xác định khi $A$ lấy giá trị không âm và ta thường viết là $A \ge 0$.
$A \ge 0$ là điều kiện xác định hay điều kiện có nghĩa của $\sqrt A$.
Ví dụ 5. Xét căn thức $P = \sqrt{2x + 1}$.
a) Tìm điều kiện xác định của căn thức $P$.
b) Tính giá trị của căn thức $P$ tại $x = 0$.
Lời giải
a) Điều kiện xác định của căn thức là $2x + 1 \ge 0$.
b) Tại $x = 0$ (thỏa mãn điều kiện xác định) căn thức có giá trị:
$P = \sqrt{2.0 + 1} = 1$.
Hằng đẳng thức
⚡Với $A \ge 0$, ta có $A \ge 0$; $\big(\sqrt A\big)^2 = A$.
⚡$\sqrt{A^2} = |A|$.
Ví dụ 6. Rút gọn các biểu thức $\Big(\sqrt{1 - x}\Big)^2$ với $x < 0$.
Lời giải
Từ giả thiết $x < 0$ suy ra $1 - x > 0$.
Do đó, $\Big(\sqrt{1 - x}\Big)^2 = 1 - x$.