Bài tập tự luận SVIP

Hướng dẫn giải:

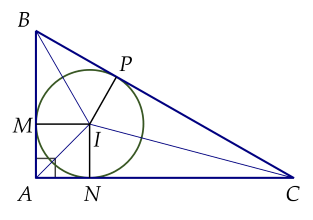
Đường tròn $( I;r )$ tiếp xúc với các cạnh $AB, \, AC, \, BC$ theo thứ tự $M, \, N, \, P$.

Ta có: $S_{AIB}=\dfrac12IM.AB=\dfrac12r.AB$ (1);

$S_{AIC}=\dfrac12IN.AC=\dfrac12r.AC$ (2);

$S_{BIC}=\dfrac12r.BC$ (3)

Cộng vế theo vế của (1), (2) và (3), ta được: $\dfrac{S_{AIB}+S_{AIC}+S_{BIC}}{S_{ABC}}=\dfrac12r.( AB+AC+BC)$

Mà $S_{ABC}=\dfrac12AB.AC=\dfrac{6.8}{2}=24$ cm², $BC=\sqrt{6^2+8^2}=\sqrt{100}=10$ cm

Nên ta có: $24=\dfrac12r( 6+8+10 )$ suy ra $r=2$ (cm).

Hướng dẫn giải:

Gọi $D, \, E,\, F$ là tiếp điểm của đường tròn $( I )$ với $AB$

$\Delta ABC$ vuông tại $A$, theo định lí Pythagore ta có: $BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=15$ cm

Theo tính chất của hai tiếp tuyến cắt nhau, ta có: $AD=AF; \, BD=BE; \, CE=CF$.

Do đó $2AD+2BE+2CE=AB+BC+CA=9+12+15=36$

$2AD+2BC=36$

$AD=3$ (cm) suy ra $BD=6$ (cm); $DI=3$ cm.

Gọi $N=BI\cap AC$, ta có: $\dfrac{BI}{BN}=\dfrac{BD}{BA}=\dfrac{6}{9}=\dfrac{2}{3}=\dfrac{BG}{BM}$

Suy ra $IG$ // $NM$ và $IG=\dfrac{2}{3}NM$.

Ta có $\diamond IDAF$ là hình vuông, có: $\dfrac{BD}{BA}=\dfrac{DI}{AN}=\dfrac{2}{3}$

Suy ra $AN=4,5$ cm.

Mà $M$ là trung điểm của $AC$ nên: $NM=AM-AN=6-4,5=1,5$ (cm) suy ra $IG=1$ cm.

Hướng dẫn giải:

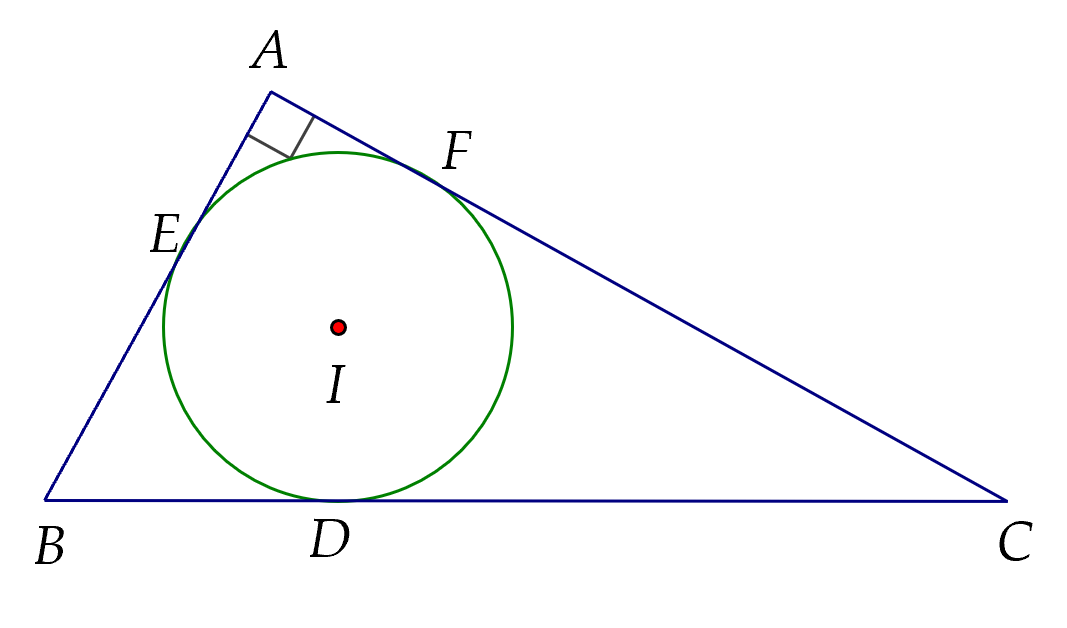
a) Gọi $E, \, F$ là tiếp điểm của đường tròn $(I)$ với các cạnh $AB, \, AC$

Theo tính chất của hai tiếp tuyến cắt nhau, ta có: $AE=AF; \, BE=BD; \, CD=CF$

Do đó: $2BD=BD+BE=BC-CD+AB-AE$

$=BC+AB-(CD+AE)=BC+AB-(CF+AF)$

$=BC+AB-AC$ suy ra $BD=\dfrac{BC+AB-AC}{2}$

b) Tương tự câu a) ta có: $DC=\dfrac{BC+AC-AB}{2}$ mà $AB^2+AC^{2}=BC^2$ ($\Delta ABC$ vuông tại $A$), do đó:

$BD.DC=\dfrac{(BC+AB-AC)(BC+AC-AB)}{4}$

$\dfrac{BC^2-(AB-AC)^2}{4}=\dfrac{BC^2-AB^2-AC^2+2AB.AC}{4}$

$=\dfrac{AB.AC}{2}={{S}_{ABC}}$.

Hướng dẫn giải:

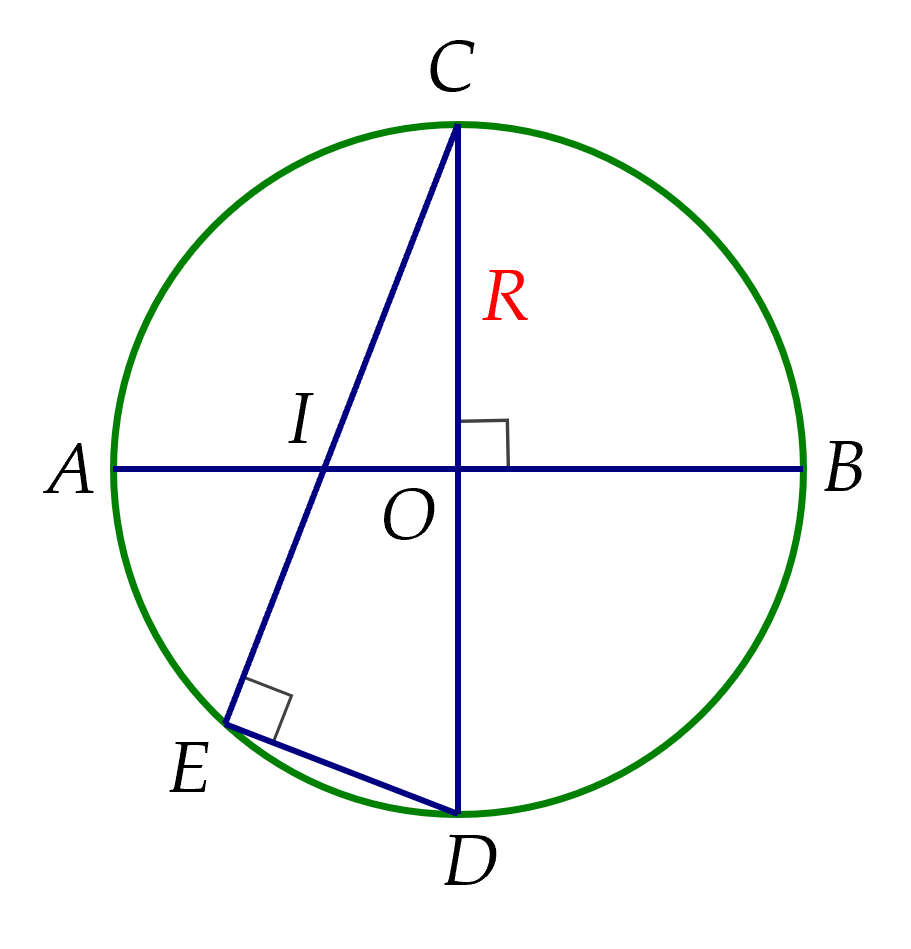
Ta có $AI=\dfrac{2AO}{3}=\dfrac{2R}{3}$ suy ra $OI=R-\dfrac{2R}{3}=\dfrac{R}{3}$

$\Delta OCI$ vuông tại $O$, ta có:

$CI=\sqrt{O{{C}^{2}}+O{{I}^{2}}}=\sqrt{R^2+\Big( \dfrac{R}{3} \Big)^2}=\dfrac{R\sqrt{10}}{3}$ nội tiếp đường tròn  có cạnh $CD$ là đường kính

Suy ra $\Delta CED$ vuông tại $E$

Hai tam giác vuông $OCI$ và $CED$ có $\widehat{C}$ :chung 

Suy ra $\Delta COI \backsim \Delta CED$

Suy ra $\dfrac{CO}{CE}=\dfrac{CI}{CD}$

$CE=\dfrac{CO.CD}{CI}=\dfrac{R.2R}{R\dfrac{\sqrt{10}}{3}}=\dfrac{6R}{\sqrt{10}}=\dfrac{3R\sqrt{10}}{5}$.