Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình hoành độ giao điểm:
2 x + 1 x + 1 = x + m - 1 ( x ≠ - 1 ) ⇔ x 2 + ( m - 2 ) x + ( m - 2 ) = 0 ( * )
Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt khác - 1
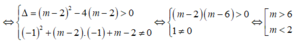
Khi đó d cắt ( C) tại A( x1; x1+ m- 1) ; B ( x2; x2+ m- 1)
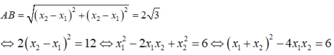
Áp dụng định lý Vi-et x 1 + x 2 = - m + 2 x 1 x 2 = m - 2 ta có:
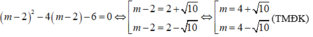
Vậy m = 4 ± 10
Chọn B.

Phương trình hoành độ giao điểm của ( C) và d là
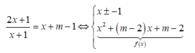
Để ( C) cắt ( d) tại hai điểm phân biệt khi và chỉ khi f( x) =0 có hai nghiệm phân biệt
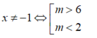
Gọi A( x1; y1) ; B( x2; y2) là giao điểm của ( C) và d
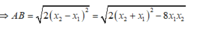
Theo hệ thức Viet, ta được
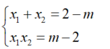
mà
![]()
Chọn D.

Chọn C
Ta có: y ' = 2 x 2 - 2 m x - 2 ( 3 m 2 - 1 )
g ( x ) = x 2 - m x - 3 m 2 + 1 là tam thức bậc hai có ∆ = 13 m 2 - 4
Do đó hàm số có hai điểm cực trị khi và chỉ khi y ' có hai nghiệm phân biệt
⇔ g ( x ) có hai nghiệm phân biệt

x 1 ; x 2 là các nghiệm của g(x) nên theo định lý Vi-ét, ta có
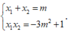

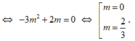
Đối chiếu với điều kiện (1), ta thấy chỉ m = 2 3 thỏa mãn yêu cầu bài toán

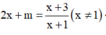



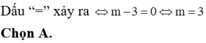




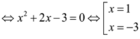
Hình như thiếu đề là M,N nguyên nữa bạn