
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


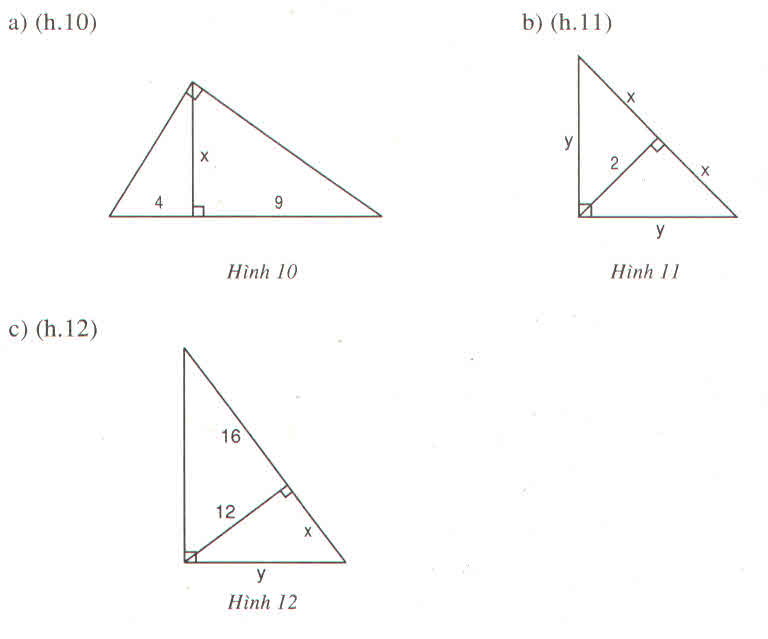
a) Ta có: x² = 4.9 = 36 => x = 6
b) Ta có: * 2² = x.x => x² = 4 => x = 2
* y² = x(x + x) = 2.4 = 8 => y = 2√2
c) Ta có: 12² = x.16 => x = 144/16 = 9
Vậy x = 9
y² = x(x + 16) = 6(9 + 16) = 9.25 = 225 => y = 15
a) Dùng hệ thức 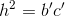 . Đáp số
. Đáp số 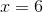
b) Dùng hệ thức 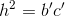 tính được
tính được 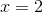 . Để tìm y, có thể dùng hệ thức
. Để tìm y, có thể dùng hệ thức 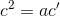 hoặc định lý Py-ta-go. ĐS
hoặc định lý Py-ta-go. ĐS 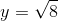
c) Dùng hệ thức 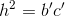 tính được
tính được 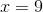 từ đó
từ đó 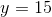 .
.

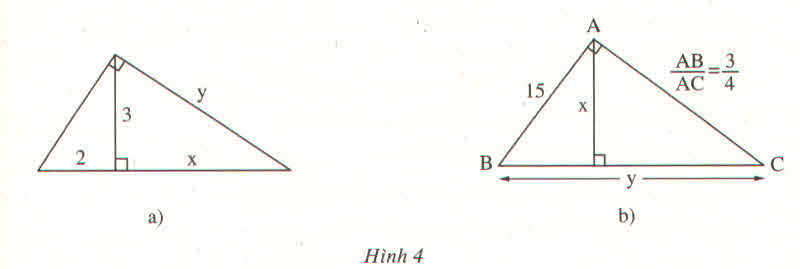
a) Áp dụng hệ thức lượng trong tam giác vuông⇒32=2x⇒x=\(\dfrac{9}{2}=4,5\)
Áp dụng định lý Pi-ta-go⇒y2=32+x2=9+20,25=29,25⇒\(y=\dfrac{3\sqrt{13}}{2}\)
b) Ta có \(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AC=\dfrac{4}{3}.AB=\dfrac{4}{3}.15=20\)
Áp dụng hệ thức lượng trong tam giác vuông ⇒\(\dfrac{1}{x^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{225}+\dfrac{1}{400}=\dfrac{1}{144}\Rightarrow x^2=144\Rightarrow x=12\)Áp dụng hệ thức lượng trong tam giác vuông ⇒AB.AC=x.y⇒\(y=\dfrac{AB.AC}{x}=\dfrac{15.20}{12}=25\)

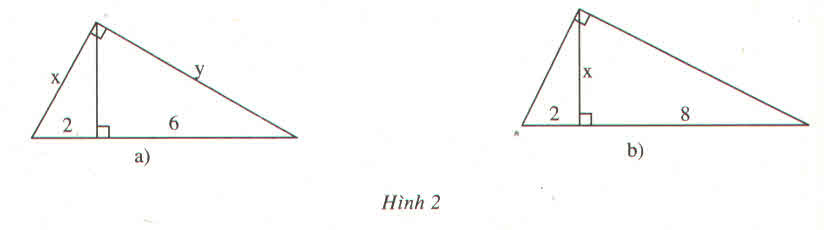
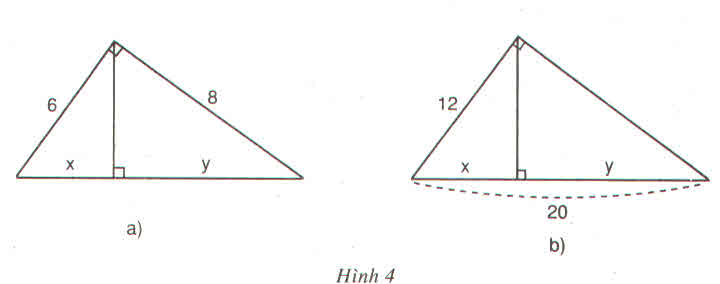
a) Hình a
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
x2=2.(2+6)=2.8=16 ⇒x=4x2=2.(2+6)=2.8=16⇒x=4
y2=6.(2+6)=6.8=48⇒y=√48=4√3y2=6.(2+6)=6.8=48⇒y=48=43
b) Hình b
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
x2=2.8=16⇒x=4

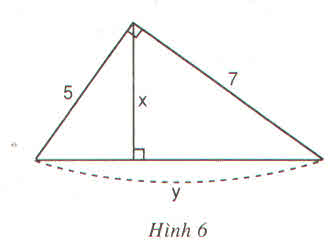
a)Áp dụng hệ thức lượng trong tam giác ta có:
72 = y(x+y)
52 = x(x+y)
=> (x+y)2=52+72=25+49=74
Do x,y là độ dài cạnh tam giác nên x>0 y>0
=>x+y=\(\sqrt{74}\)
=>x = \(25:\sqrt{74}=\dfrac{25\sqrt{74}}{74}\)
y = \(49:\sqrt{74}=\dfrac{49\sqrt{74}}{74}\)
b)Áp dụng hệ thức lượng trong tam giác ta có:
y(x+y) = 142 = 196
x+y=16(giả thiết)
=> y = 196:16 = 12,25
=> x = 16-12,25=3,75


Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều

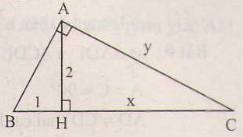
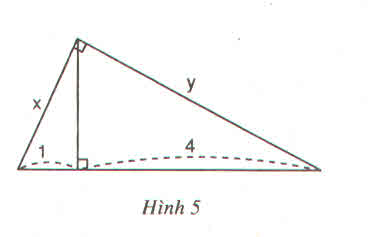
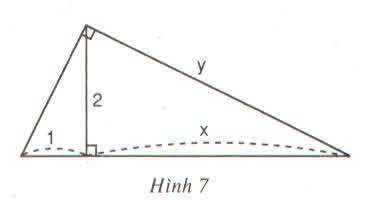
Đặt tên các đỉnh của tam giác như hình bên
Áp dụng hện thức 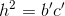 ta có:
ta có:
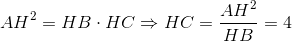
Do đó 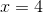
Áp dụng hệ thức 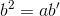 ta có
ta có
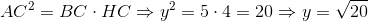
Nhận xét: Ta có thể tính y theo định lý Pi-ta-go:
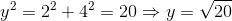 .
.

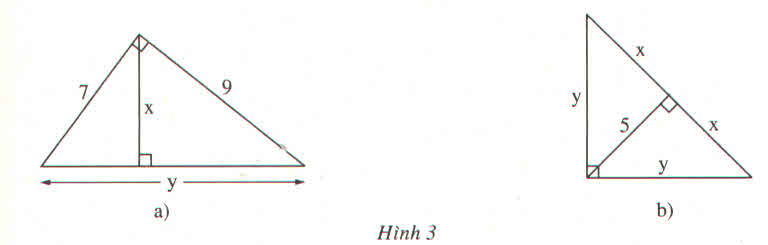
a: \(y=\sqrt{7^2+9^2}=\sqrt{130}\left(cm\right)\)
\(x=\dfrac{7\cdot9}{\sqrt{130}}=\dfrac{63\sqrt{130}}{130}\left(cm\right)\)
b: \(x\cdot x=5^2\)
nên x=5(cm)
\(y=\sqrt{25+25}=5\sqrt{2}\)
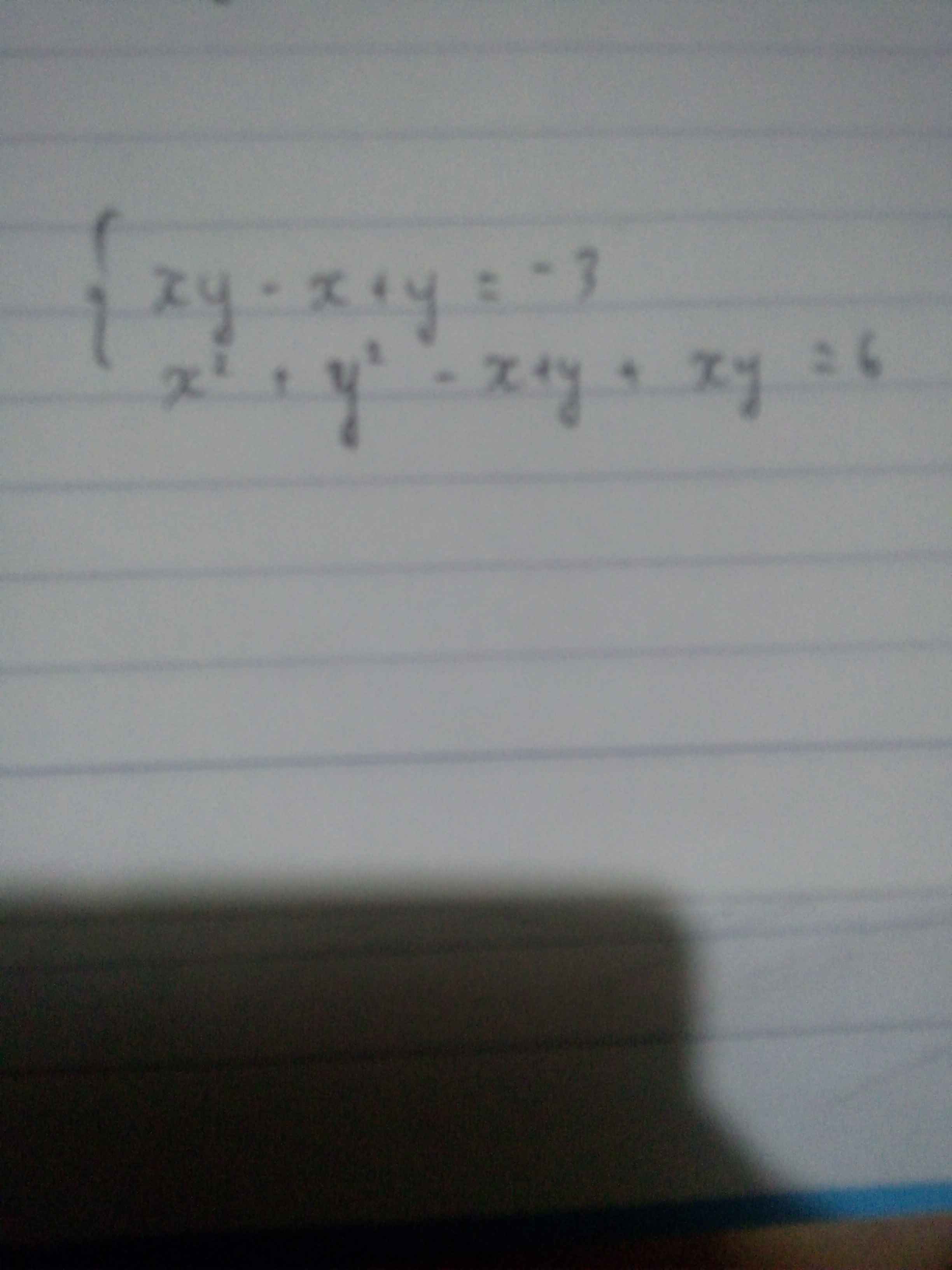

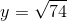 .
.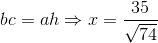 .
.

\(\Leftrightarrow\left\{{}\begin{matrix}3xy-3\left(x-y\right)=-9\\x^2+y^2+xy-\left(x-y\right)=6\end{matrix}\right.\)
Trừ vế cho vế:
\(x^2+y^2-2xy+2\left(x-y\right)=15\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)-15=0\Rightarrow\left[{}\begin{matrix}x-y=3\\x-y=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=x-3\\y=x+5\end{matrix}\right.\)
Thế vào pt đầu:
\(\Rightarrow\left[{}\begin{matrix}x\left(x-3\right)-x+x-3=-3\\x\left(x+5\right)-x+x+5=-3\end{matrix}\right.\)
\(\Leftrightarrow...\)