NH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VD
1
4 tháng 5 2016
Tập xác định \(D=R\)
Ta có : \(y'=3^x\ln3\left(\sqrt{x^2+1}-x\right)+3^x\left(\frac{x}{\sqrt{x^2+1}}-1\right)\)
\(=3^x\left(\sqrt{x^2+1}-x\right)\left(\ln3-\frac{1}{\sqrt{x^2+1}}\right)\)
Ta có : \(\begin{cases}\sqrt{x^2+1}-x>\sqrt{x^2-x}\ge0\\\ln3>1>\frac{1}{\sqrt{x^2+1}}\Rightarrow\ln3-\frac{1}{\sqrt{x^2+1}}>0\end{cases}\)
\(\Rightarrow y'>0\) với mọi x
Vậy hàm số đồng biến trên R
HN
20 tháng 10 2021
Tập xác định: D=\(\left[-2\sqrt{2};2\sqrt{2}\right]\).
\(y'=1-\dfrac{x}{\sqrt{8-x^2}}\) = 0 \(\Rightarrow\) x=2.
Bảng biến thiên:
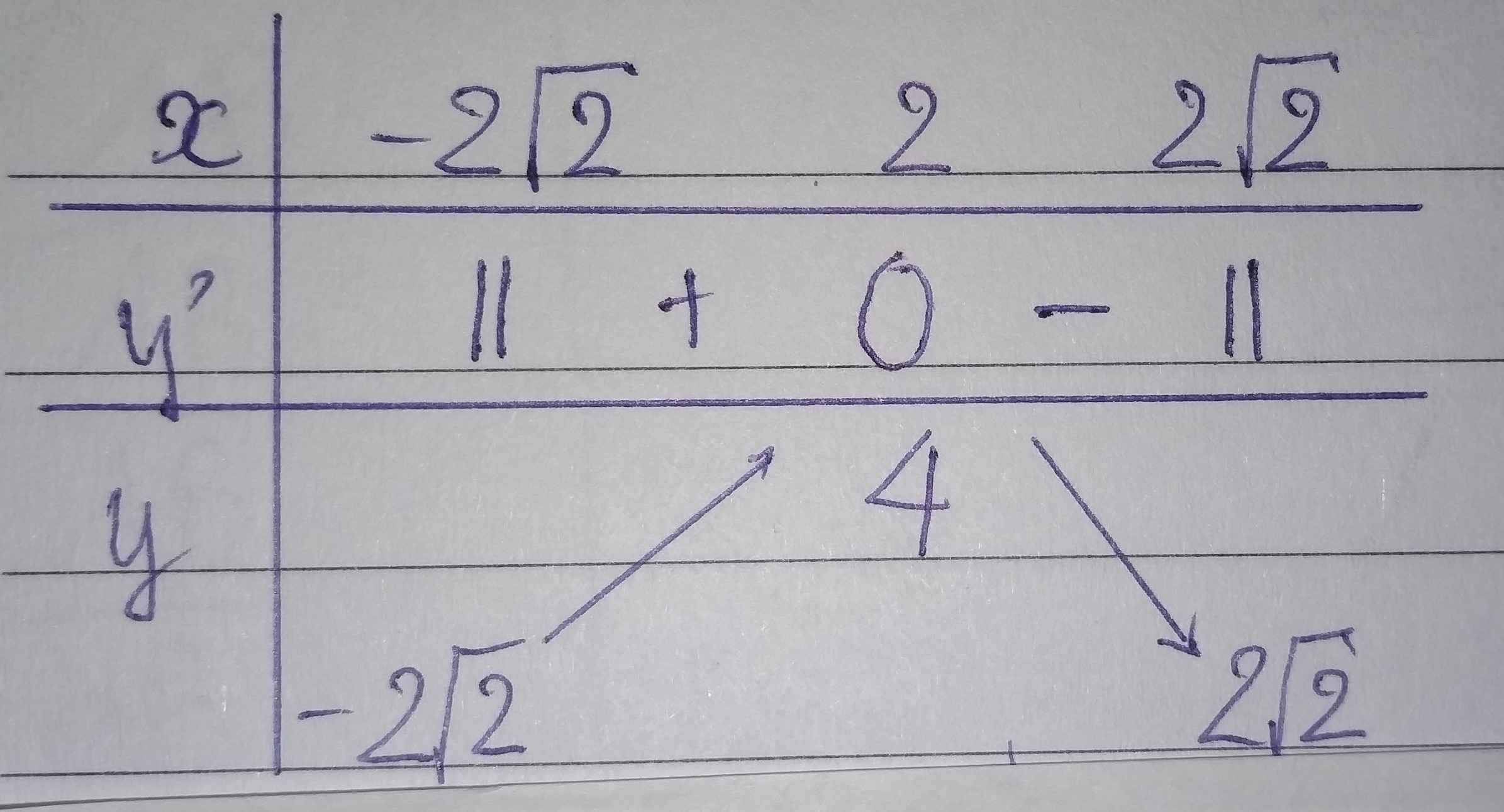
Vậy hàm số đã cho đồng biến trên khoảng (\(-2\sqrt{2}\);2), nghịch biến trên khoảng (2;\(2\sqrt{2}\)) và yCĐ=4 (tại x=2).
Tham khảo: Đồ thị:
3 tháng 8 2020
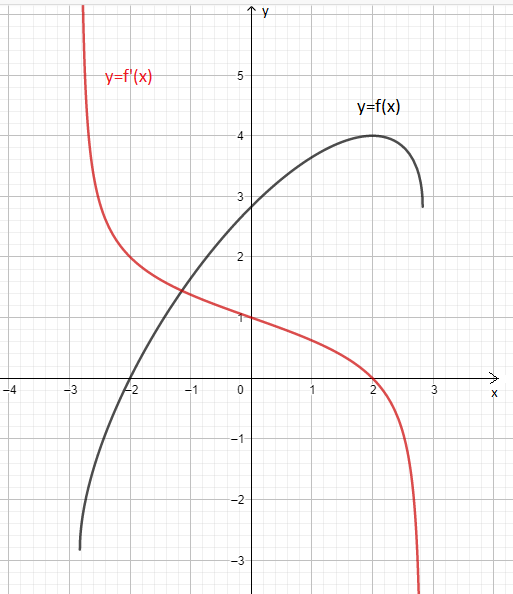
Bạn kiểm tra lại đề. Và vào hoc 24 để đăng nhé!
Làm câu cuối:
TXĐ: \(x\in\)[ 0 ; + vô cùng )
\(y'=\frac{1}{2\sqrt{x}}-1=0\Leftrightarrow2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}\left(tm\right)\)
Vẽ bảng biến thiên:
....
Từ bảng biên thiên:
Hàm số đồng biến trong khoảng ( 0 ; 1/4 )
Hàm số nghịch biên trong khoảng ( 1/4 ; + dương vô cùng)
BT
1
ND
1
6 tháng 5 2016
Tập xác định \(x< \frac{1}{2}\)
Ta có : \(y'=1-\frac{2}{1-2x}=\frac{-1-2x}{1-2x}\Rightarrow y'=0\Leftrightarrow x=-\frac{1}{2}\)
Hàm số đồng biến trên \(\left(-\infty;-\frac{1}{2}\right)\)
Hàm số nghịch biến trên \(\left(-\frac{1}{2};\frac{1}{2}\right)\)
NT
2
8 tháng 9 2023
\(f\left(x\right)=x+\sqrt[]{x^2-4}\)
\(f\left(x\right)\) xác định khi và chỉ khi
\(x^2-4\ge0\Leftrightarrow x^2\ge4\Leftrightarrow x\le-2\cup x\ge2\)
Tập xác định : \(D=(-\infty;-2]\cup[2;+\infty)\)
\(f'\left(x\right)=1+\dfrac{x}{\sqrt[]{x^2-4}}\)
\(f'\left(x\right)=0\)
\(\Leftrightarrow1+\dfrac{x}{\sqrt[]{x^2-4}}=0\)
\(\Leftrightarrow\dfrac{\sqrt[]{x^2-4}+x}{\sqrt[]{x^2-4}}=0\)
\(\Leftrightarrow\sqrt[]{x^2-4}+x=0\left(x< -2;x>2\right)\)
Theo bất đẳng thức Bunhiacopxki:
\(\left(1.\sqrt[]{x^2-4}+1.x\right)^2\le2\left(2x^2+4\right)=4\left(x^2+2\right)\)
\(pt\Leftrightarrow4\left(x^2+2\right)=0\left(vô.lý\right)\)
\(\Rightarrow\) phương trình vô nghiệm
8 tháng 9 2023
Tiếp tục bài giải, mình nhấn nút gửi
\(...\Rightarrow f'\left(x\right)>0,\forall x\in D\)
\(\Rightarrow f\left(x\right)\) luôn luôn tăng trên tập xác định D.
ND
1
6 tháng 5 2016
Ta có :\(y'=\left(6x-2\right)e^{3x^2-2x-x}\)
Hàm đồng biến trên \(\left(\frac{1}{3};+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;\frac{1}{3}\right)\)
HT
25 tháng 8 2016
Xét tính chẵn lẻ:
a) TXĐ: D = R \ {π/2 + kπ| k nguyên}
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{3\tan^3\left(-x\right)-5\sin\left(-x\right)}{2+\cos\left(-x\right)}=-\frac{3\tan^3x-5\sin x}{2+\cos x}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
b) TXĐ: D = R \ \(\left\{\pm\sqrt{2};\pm1\right\}\)
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{\sin\left(-x\right)}{\left(-x\right)^4-3\left(-x\right)^2+2}=-\frac{\sin x}{x^4-3x^2+2}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
HT
25 tháng 8 2016
Tìm GTLN, GTNN:
TXĐ: D = R
a) Ta có (\(\left(\sin x+\cos x\right)^2=1+\sin2x\)
Với mọi x thuộc D ta có\(-1\le\sin2x\le1\Leftrightarrow0\le1+\sin2x\le2\Leftrightarrow0\le\left(\sin x+\cos x\right)^2\le2\)
\(\Leftrightarrow0\le\left|\sin x+\cos x\right|\le\sqrt{2}\Leftrightarrow-\sqrt{2}\le\sin x+\cos x\le\sqrt{2}\)
Vậy \(Min_{f\left(x\right)}=-\sqrt{2}\) khi \(\sin2x=-1\Leftrightarrow2x=-\frac{\pi}{2}+k2\pi\Leftrightarrow x=-\frac{\pi}{4}+k\pi\)
\(Max_{f\left(x\right)}=\sqrt{2}\) khi\(\sin2x=1\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
b) Với mọi x thuộc D ta có:
\(-1\le\cos x\le1\Leftrightarrow-2\le2\cos x\le2\Leftrightarrow1\le2\cos x+3\le5\)
\(\Leftrightarrow1\le\sqrt{2\cos x+3}\le\sqrt{5}\Leftrightarrow5\le\sqrt{2\cos x+3}+4\le\sqrt{5}+4\)
Vậy\(Min_{f\left(x\right)}=5\) khi \(\cos x=-1\Leftrightarrow x=\pi+k2\pi\)
\(Max_{f\left(x\right)}=\sqrt{5}+4\) khi \(\cos x=1\Leftrightarrow x=k2\pi\)
c) \(y=\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x\cos^2x\)\(=1-\frac{1}{2}\left(2\sin x\cos x\right)^2=1-\frac{1}{2}\sin^22x\)
Với mọi x thuộc D ta có: \(0\le\sin^22x\le1\Leftrightarrow-\frac{1}{2}\le-\frac{1}{2}\sin^22x\le0\Leftrightarrow\frac{1}{2}\le1-\frac{1}{2}\sin^22x\le1\)
Đến đây bạn tự xét dấu '=' xảy ra khi nào nha :p
Lời giải:
MXĐ: \(x\in [2;4]\)
Ta có với \(x\neq 2; x\neq 4\) thì:
\(y'=(\sqrt{x-2}+\sqrt{4-x})'=\frac{1}{2\sqrt{x-2}}-\frac{1}{2\sqrt{4-x}}\)
\(y'=0\Leftrightarrow \sqrt{4-x}=\sqrt{x-2}\Leftrightarrow x=3\)
Lập bảng biến thiên ta suy ra hàm số đồng biến trên \((2;3)\), nghịch biến trên \((3,4)\)
Bảng biến thiên: