
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
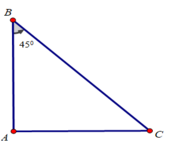
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1
b)
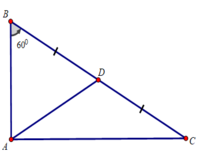
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 60o
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3

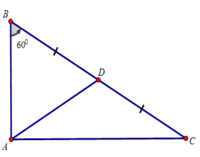
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 60o
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3

a) Mình nghĩ là cos a = cot a . sin a chứ :))
CM nà :
Ta có : cot a = \(\frac{AB}{AC}\)(1)
\(\frac{cosa}{sina}=\frac{AB}{BC}:\frac{AC}{BC}=\frac{AB}{AC}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\)cot a = \(\frac{cosa}{sina}\)
\(\Leftrightarrow\)cos a = cot a . sin a
b) Ta có : tan a = \(\frac{AC}{AB}\)
Lại có : cot a = \(\frac{AB}{AC}\)
\(\Rightarrow\)cos a . tan a = \(\frac{AC.AB}{AB.AC}\)= 1
Vậy ...

Áp dụng định lí Ceva cho tam giác ABC có 3 cát tuyến AH,BM,CD đồng quy: \(\frac{MA}{MC}.\frac{HC}{HB}.\frac{DB}{DA}=1\Rightarrow\frac{HC}{HB}=\frac{AD}{BD}\)
(Vì M trung điểm AC nên \(\frac{MA}{MC}=1\))
(Định lí Ceva này bạn có thể lên google search để nắm rõ, Định lí này chỉ học sinh trong đội tuyển mới học thoi)
Vì CD là phân giác \(\widehat{BCA}\)nên \(\frac{CA}{CB}=\frac{DA}{DB}\Rightarrow\frac{AC}{BC}=\frac{HC}{HB}=\frac{BC-HB}{HB}=\frac{BC}{HB}-1\)
\(\Rightarrow AC=\frac{BC^2}{HB}-BC=\frac{AB^2+AC^2}{HB}-BC=\frac{HB.BC+AC^2}{HB}-BC=\frac{AC^2}{HB}\Rightarrow AC=HB\)
( Chỗ này áp dụng định lí Pythagoras: BC2 = AB2+AC2 và Hệ thức lượng tam giác vuông AB2=HB.BC)
Có \(\hept{\begin{cases}AB^2=HB.BC\\BC^2=AB^2+AC^2\end{cases}\Rightarrow\hept{\begin{cases}AB^2=aAC\\AB^2=a^2-AC^2\end{cases}}\Rightarrow\hept{\begin{cases}AB=\sqrt{aAC}\\AC^2+aAC-a=0\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}AC=\frac{-a+\sqrt{a^2+4a}}{2}=\frac{2a}{a+\sqrt{a^2+4a}}\\AB=\sqrt{aAC}=\sqrt{\frac{2a^2}{a+\sqrt{a^2+4a}}}\end{cases}}\)

bài 1: ta có : \(cos^220+cos^240+cos^250+cos^270\)
\(=cos^220+cos^270+cos^240+cos^250\)
\(=cos^220+cos^2\left(90-20\right)+cos^240+cos^2\left(90-40\right)\)
\(=cos^220+sin^220+cos^240+sin^240=1+1=2\)
bài 2: a) ta có : \(cot^2\alpha-cos^2\alpha=cos^2\alpha\left(\dfrac{1}{sin^2\alpha}-1\right)=cos^2\alpha.\left(\dfrac{1-sin^2\alpha}{sin^2\alpha}\right)\)
\(=cos^2\alpha.\left(\dfrac{cos^2\alpha}{sin^2\alpha}\right)=cos^2\alpha.cot^2\alpha\left(đpcm\right)\)
b) ta có : \(sin^2\alpha+cos^2\alpha=1\Leftrightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Leftrightarrow\dfrac{1+cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1-cos\alpha}\left(đpcm\right)\)
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1