Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x=3 có: 3(m-1) -m+5 =0
3m-3-m+5 =0 => m = -1
b) nếu m=1 có: (m-1)x = 0 => (m-1)x -m +5 = 0 => 4=0 vô lý
c) (m-1)x -m+5 =0 => x = (m-5)/(m-1)
+ nếu m=1 vô nghiệm
+ m khác 1 pt có nghiệm x =(m-5)/(m-1)

a/\(\Leftrightarrow\frac{\left(x-1\right)\left(x-4\right)}{x-1}+\frac{x^2-8x+4}{2x+1}=0\)
\(\Leftrightarrow x-4+\frac{x^2-8x+4}{2x+1}=0\)
\(\Leftrightarrow\left(x-4\right)\left(2x+1\right)+x^2-8x+4=0\)
\(\Leftrightarrow3x^2-15x=0\Leftrightarrow x\left(x-5\right)=0.....\)Vậy x=0, x=5

b/\(\Leftrightarrow\frac{m\left(x+m\right)}{x^2-m^2}-\frac{3m^2-4m+3}{x^2-m^2}=\frac{x-m}{x^2-m^2}\)
\(\Leftrightarrow mx+m^2-3m^2+4m-3=x-m\)
\(\Leftrightarrow-2m^2+mx+5m-x-3=0\)
\(\Leftrightarrow\left(-2m^2+2m+3m-3\right)+x\left(m-1\right)=0\)
\(\Leftrightarrow-2m\left(m-1\right)+3\left(m-1\right)+x\left(m-1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(x-2m+3\right)=0\Rightarrow\left[{}\begin{matrix}m=1\left(1\right)\\x=2m-3\left(2\right)\end{matrix}\right.\)
(ĐKXĐ x khác +-m)
-Với (1) PT đúng với mọi x
-Với (2), PT TM khi \(x=2m-3\ne+-m\Leftrightarrow\left\{{}\begin{matrix}m-3\ne0\\3m-3\ne0\end{matrix}\right.\)
Vậy (2) là nghiệm khi m khác (3,1)

Bài làm
a) 3x - 1 = 2x + 4
<=> x = 5
Vậy x = 5 là nghiệm phương trình.
b) x( x + 3 ) = ( 2x + 1 )( x + 3 )
<=> x( x + 3 ) - ( 2x + 1 )( x + 3 ) = 0
<=> ( x + 3 )( x - 2x - 1 ) = 0
<=> ( x + 3 )( -x - 1 ) = 0
<=> x + 3 = 0 hoặc -x - 1 = 0
<=> x = -3 hoặc x = -1
Vậy x = -3 hoặc x = -1 là tập nghiệm phương trình
c) quy đồng mẫu ra r lm, bh ngủ.

Bài 1:
a.
Thay x = 1 là nghiệm của pt, ta được:
\(1^3+a.1^2-4.1-4=0\)
\(\Leftrightarrow1+a-4-4=0\)
\(\Leftrightarrow1+a-8=0\)
\(\Leftrightarrow a-7=0\)
\(\Leftrightarrow a=7\)
b.
Với a = 7 ta được:
\(x^3+7x^2-4x-4=0\)
\(\Leftrightarrow x^3-x^2+8x^2-8x+4x-4=0\)
\(\Leftrightarrow x^2\left(x-1\right)+8x\left(x-1\right)+4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^2+8x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2+8x+4=0\end{matrix}\right.\)
Ta có:
\(x^2+8x+4=x^2+2.x.4+4^2-12\)
\(=\left(x+4\right)^2-12=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4+2\sqrt{3}\\x=-4-2\sqrt{3}\end{matrix}\right.\)
Vậy. \(\left[{}\begin{matrix}x=1\\x=-4+2\sqrt{3}\\x=-4-2\sqrt{3}\end{matrix}\right.\)

Bài 1:
a) \(\left(m+2\right).3-5=4\)
\(\Leftrightarrow3m+6-5=4\)
\(\Leftrightarrow3m+1=4\)
\(\Leftrightarrow3m=4-1\)
\(\Leftrightarrow3m=3\)
\(\Leftrightarrow m=1\)
Vậy: m = 1
b) \(\left(m-3\right).\left(-2\right)+8=-10\)
\(\Leftrightarrow-2m+6+8=-10\)
\(\Leftrightarrow-2m+14=-10\)
\(\Leftrightarrow-2m=-10-14\)
\(\Leftrightarrow-2m=-24\)
\(\Leftrightarrow m=12\)
Vậy: m = 12
Bài 2:
a) \(\left(x-2\right)^2=9\)
\(\Leftrightarrow\left(x-2\right)^2=3^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
b) \(\left(x+3\right)^2-0,16=0\)
\(\Leftrightarrow\left(x+3\right)^2=0,16\)
\(\Leftrightarrow\left(x+3\right)^2=\left(0,4\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0,4\\x+3=-0,4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2,6\\x=-3,4\end{matrix}\right.\)
c) \(x^3=25x\)
\(\Leftrightarrow x^3-25x=0\)
\(\Leftrightarrow x\left(x^2-25\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-25=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm5\end{matrix}\right.\)

\(2m\left(x-3\right)+1=x-5\)
\(\Leftrightarrow\left(2m-1\right)x=6m-6\)
Để phương trình có nghiệm duy nhất thì \(2m-1\ne0\Leftrightarrow m\ne\frac{1}{2}\).
Vậy \(m\ne\frac{1}{2}\)thì phương trình đã cho có nghiệm duy nhất.


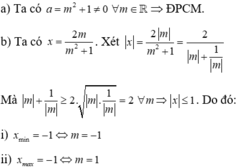
a)thay x=-3 vào phương trình ta được:
\(\left(m-1\right)\left(-3\right)-m+5=0\\ \Leftrightarrow-3m+3-m+5=0\Leftrightarrow-4m=-3-5=-8\\ \Leftrightarrow m=\dfrac{-8}{-4}=2\)
Vậy tại m=2 thì x=-3 là nghiệm của phương trình
b)thay m=1 vào phương trình ta được:
\(\left(1-1\right)x-1+5=0\\ \Leftrightarrow0x+4=0\)
Vậy phương trình vô nghiệm
c) ta có: phương trình có dạng ax+b=0 với a=m-1 và b=-m+5
T/H 1: \(a\ne0\Leftrightarrow m-1\ne0\Leftrightarrow m\ne1\Rightarrow\)phương trình có nghiệm duy nhất:
x=\(-\dfrac{b}{a}=\dfrac{-\left(-m+5\right)}{m-1}=\dfrac{m+5}{m-1}\)
Vậy S={(m+5)/(m-1)}
T/H 2: a=0 phương trình có dạng 0a+b=0
1.\(\left\{{}\begin{matrix}a=0\\b\ne0\end{matrix}\right.\Leftrightarrow m=1\)(dĩ nhiên m khác -5) \(\Rightarrow\)phương trình có dạng 0x=b
Vậy phương trình vô ngiệm, S=\(\varnothing\)
2.a=0,b=0: không có giá trị m thỏa mãn
Vậy tại m khác 1 phương trình có nghiệm duy nhất là \(S=\left\{\dfrac{m+5}{m-1}\right\}\)