Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Xác định chiều cao hình chóp bằng kiến thức 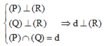
Xác định khoảng cách ![]()
Tính toán bằng cách sử dụng quan hệ diện tích, định lý hàm số cosin, công thức tính diện tích tam giác S =
1
2
a.h với a là cạnh đáy, h là chiều cao tương ứng và ![]()
Cách giải:
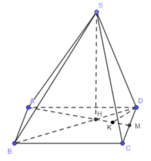
Gọi H = AM ∪ BD
Ta có 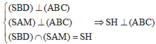
Vì AB//CD nên theo định lý Ta-lét ta có

Ta có ![]()
![]()
![]()
Vì M là trung điểm của DC và ABCD là hình bình hành có diện tích 2 a 2 nên ta có:
![]()
Lại có CD = AB = a
2
![]()
Khi đó ![]()
![]()
![]()
![]()
![]()
![]()
Lại có ![]()
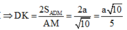
Từ đó ![]()
Chọn: C

Chọn A

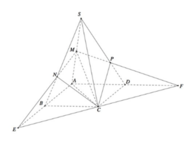
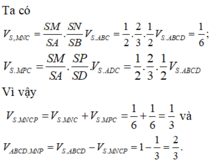
Cách 2: Dùng công thức tính nhanh tỷ số thể tích
Có
![]()
![]()
Vì Vậy
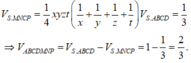

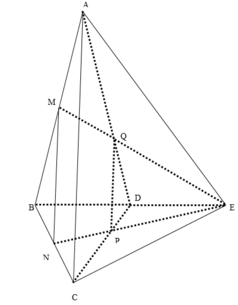
Gọi I là trung điểm AD \(\Rightarrow SI\perp AD\Rightarrow SI\left(ABCD\right)\Rightarrow d\left(I;\left(ABCD\right)\right)=SI\)
Ta có \(SM\cap\left(ABCD\right)=\left\{B\right\}\) và \(\frac{SB}{MB}=2\) nên \(d\left(M;\left(ABCD\right)\right)=\frac{1}{2}d\left(I;\left(ABCD\right)\right)=\frac{1}{2}SI=\frac{1}{2}\cdot\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\)
\(S_{CNP}=\frac{1}{2}\cdot CN\cdot CP=\frac{1}{2}\cdot\frac{1}{2}CD\cdot\frac{1}{2}\cdot BC=\frac{a^2}{8}\)
\(V_{M.CNP}=\frac{1}{3}\cdot d\left(M;\left(ABCD\right)\right)\cdot S_{CNP}=\frac{a^3\sqrt{3}}{96}\)

có
Gắn vào hệ trục Oxyz có
CÓ : S(0,0,0) A(0,0,a) , B(0,a,0), C(a,0,0)
e nhớ ko lầm là a đã học tới bài này âu mà sao bik làm hay z???

Chọn đáp án D
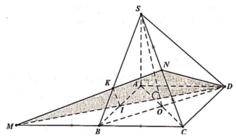
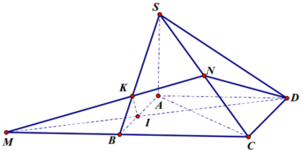
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 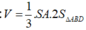
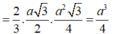
Ta có: N là trung điểm SC nên 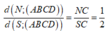
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
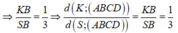
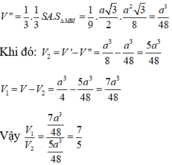


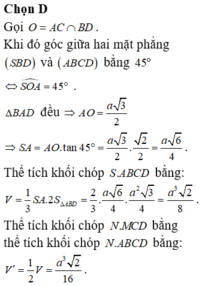
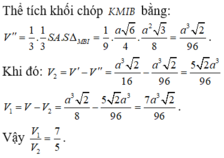

ko bít