Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

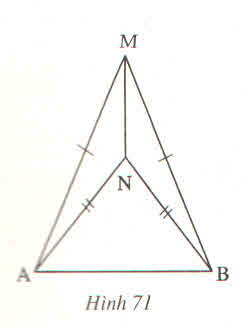
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
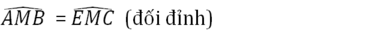
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


A E D B C
\(a)\)Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{A}:\) chung
\(AD=AE\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta ACD\left(c.g.c\right)\)
\(\Rightarrow BE=CD\)(2 cạnh tương ứng)
\(b)AB=DA+DB\)
\(AC=EA+EC\)
Mà \(AB=AC;AD=AE\)
\(\Rightarrow DB=EC\)
Xét \(\Delta BOD\) và \(\Delta COE\) có:
\(\widehat{BOD}=\widehat{COE}\left(đ^2\right)\)
\(DB=EC\left(cmt\right)\)
\(\widehat{DBE}=\widehat{ECD}\left(\Delta ABE=\Delta ACD\right)\)
\(\Rightarrow\Delta BOD=\Delta COE\left(g.c.g\right)\)

a: Gọi D là giao điểm của BM và AC
Xét ΔABD có AB+AD>BD
=>AB+AD>BM+MD
Xét ΔMDC có MD+DC>MC
Do đó; AB+AD+MD+DC>BM+MD+MC
=>AB+AC+MD>BM+MC+MD
=>AB+AC>BM+MC
b: Gọi E,F lần lượt là giao điểm của MN với AB và AC
Xét ΔBEM có BM<BE+EM
Xét ΔCFN có CN<CF+FN
Xét ΔAEF có EF<AE+AF
Ta có: BM<BE+EM
CN<CF+FN
Do đó: BM+CN<BE+EM+CF+FN
=>BE+EM+CF+FN>BM+CN
=>BE+EM+CF+FN+MN>BM+CN+MN
=>BE+CF+EF>BM+CN+MN
=>BM+CN+MN<BE+CF+EF
mà BE+CF+EF<BE+CF+AE+AF=(BE+AE)+(AF+AC)=AB+AC
nên BM+CN+MN<AB+AC

x O y t M A B
a, Vì Ot là phân giác của xOy
=> xOt = tOy = xOy/2
Xét △OAM vuông tại A và △OBM vuông tại B
Có: AOM = MOB
OM là cạnh chung
=> △OAM = △OBM (cgv-gn)
b, Vì △OAM = △OBM
=> OA = OB (2 cạnh tương ứng)
=> AM = BM (2 cạnh tương ứng)
Xét △OAB có: OA = OB
=> △OAB cân tại O
Xét △ABM có: AM = BM
=> △ABM cân tại M
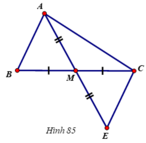
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có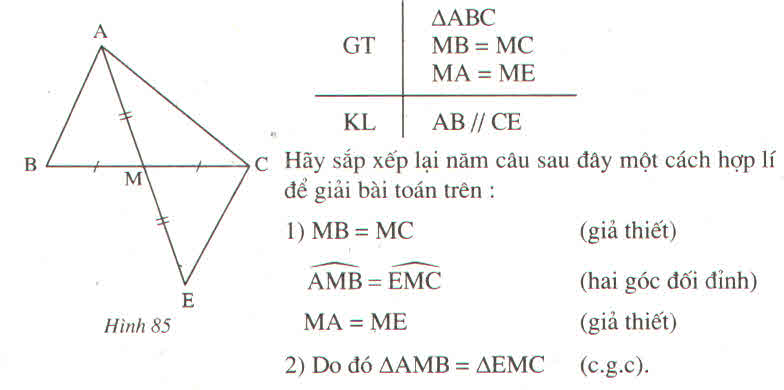
Ghi giả thiết và kết luận: