LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
1
BT
25 tháng 10 2015
Bạn Sáng nói bạn ấy chỉ mới học lớp 6 mà giải được? Đồ coi theo, đồ copy...Tui xem thường..##@@
LT
0
NH
2
PN
6 tháng 1 2016
Vì \(a\) không chia hết cho \(3\) nên \(a\) có dạng \(a=3k+1\) hoặc \(a=3k+2\) \(\left(k\in Z\right)\)
Nếu \(a=3k+1\) thì \(a^2=\left(3k+1\right)^2=9k^2+6k+1\) chia \(3\) dư \(1\)
Nếu \(a=3k+2\) thì \(a^2=\left(3k+2\right)^2=9k^2+9k+8\) chia \(3\) dư \(1\)
Vậy, nếu \(a\) không chia hết cho \(3\) thì \(a^2\) chia \(3\) dư \(1\) \(\left(1\right)\)
Tương tự, ta cũng có nếu \(b\) không chia hết cho \(3\) thì \(b^2\) chia \(3\) dư \(1\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) , suy ra \(a^2-b^2\) chia hết cho \(3\) \(\left(3\right)\)
Ta có: \(a^6-b^6=\left(a^2-b^2\right)\left[\left(a^2\right)^2+a^2b^2+\left(b^2\right)^2\right]=\left(a^2-b^2\right)\left[\left(a^2\right)^2-2a^2b^2+\left(b^2\right)^2+3a^2b^2\right]\)
\(=\left(a^2-b^2\right)\left[\left(a^2-b^2\right)+3a^2b^2\right]\)
Theo chứng minh trên, \(a^2-b^2\) chia hết cho \(3\) nên \(\left(a^2-b^2\right)^2\) chia hết cho \(3\)
Lại có: \(3a^2b^2\) chia hết cho \(3\) với mọi \(a;b\in Z\)
nên \(\left(a^2-b^2\right)+3a^2b^2\) chia hết cho \(3\) \(\left(4\right)\)
Từ \(\left(3\right)\) và \(\left(4\right)\) suy ra \(\left(a^2-b^2\right)\left[\left(a^2-b^2\right)+3a^2b^2\right]\) chia hết cho \(3.3\) hay \(a^6-b^6\) chia hết cho \(9\) \(\left(đpcm\right)\)
6 tháng 1 2016
a^6-b^6=(a^3-b^3)(a^3+b^3)=(a-b)(a^2+ab+b^2)(a+b)(a^2-ab+b^2) dung hang dang thuc
Vi a,b ko chia het cho 3 (1)
suy ra TH1 a=3k+1, b=3q+2 hoacTH2 a=3k+2, b=3q+1
TH1
a+b=3k+3q+3 chia het cho 3
a^2 va b^2 la so chinh phuong nen chia 3 du 0 hoac 1 ma a,b ko chia het cho 3
suy ra a^2, b^2 chia 3 du 1
suy ra a^2+b^2 chia 3 du 2
Lai co a=3k+1, b=3q+2 suy ra ab chia 3 du 2
Tu do suy ra a^2-ab+b^2 chia het cho 3 (2)
tu 1 va 2 so chia het cho 9
TH2 tuong tu
CM
19 tháng 6 2017
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức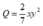 
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.
TH
29 tháng 6 2015
718+18.3-1=717.7+17.3+3-1=717+17.3-1+717.6+3=(717+17.3-1)+9.717-3.717+3
=(717+17.3-1)+9.717-3(717-1)
Ta có 717-1 chia hết cho 6 => 3(717-1) chia hết cho 18=> chia hết cho 9
Mặt khác 717+17.3-1 và 9.717 chia hết cho 9 => 718+18.3-1 chia hết cho 9
Có