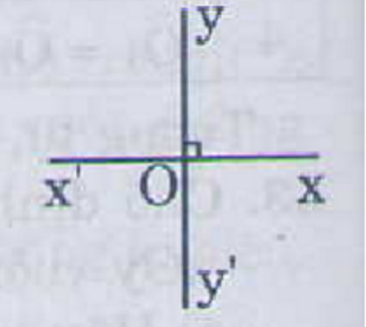Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

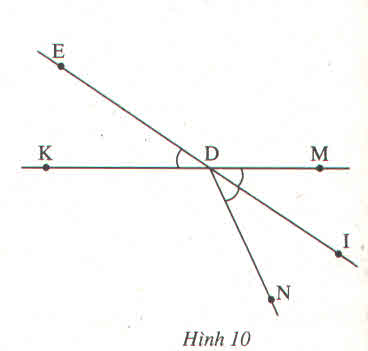
GT: DI là tia phân giác của \(\widehat{MDN}\)
\(\widehat{EDK}\) đối đỉnh với \(\widehat{IDM}\)
KL: \(\widehat{EDK}=\widehat{IDM}\)
Chứng minh (h.10)
ˆIDM=ˆIDNIDM^=IDN^ (vì DI là tia phân giác của \(\widehat{MDN}\)) (1)
ˆIDM=ˆEDKIDM^=EDK^ (vì 2 góc này đối đỉnh) (2)
Từ (1) và (2) suy ra \(\widehat{EDK}=\widehat{IDN}\)

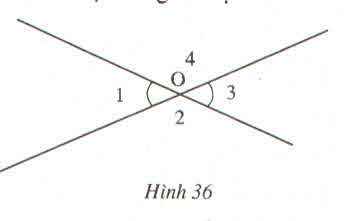
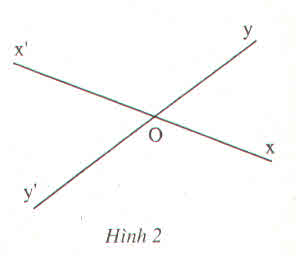
a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
ghi ngắn gọn là ( ghi mỗi đáp án)
a) X'OY'
b) là hai góc đối đỉnh
+) Của cạnh OX' và cạnh OY là tia đối của cạnh OY'


bạn ơi bạn viết rõ các góc ra đc k chứ dít quá mik k nhìn thấy để giải đc
Trả lời : 6 cặp góc đối đỉnh là :
QBy và dBx
QBc và gBx
cBd và yBg
QBd và xBy
QBg và cBx
dBg và cBy