DN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 5 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+x-2=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;4\right);\left(1;1\right)\right\}\)
HP
21 tháng 12 2020
a, Từ giả thiết suy ra \(\left\{{}\begin{matrix}a+b=-2\\-2a+b=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow y=-\dfrac{5}{3}x-\dfrac{1}{3}\)
b,
c, Phương trình hoành độ giao điểm
\(-\dfrac{5}{3}x-\dfrac{1}{3}=x-3\Leftrightarrow x=1\Rightarrow y=-2\Rightarrow M\left(1;-2\right)\)
d1, \(tanMPQ=-\left(-\dfrac{5}{3}\right)=\dfrac{5}{3}\Rightarrow\widehat{MPQ}\approx59^o\)
d2, \(P\left(-\dfrac{1}{5};0\right);Q\left(3;0\right);M\left(1;-2\right)\)
Chu vi \(P=PQ+QM+MP=\dfrac{16}{5}+2\sqrt{2}+\dfrac{2\sqrt{34}}{5}\)
\(p=\dfrac{\dfrac{16}{5}+2\sqrt{2}+\dfrac{2\sqrt{34}}{5}}{2}\)
Diện tích \(S=\sqrt{p\left(p-\dfrac{16}{5}\right)\left(p-2\sqrt{2}\right)\left(p-\dfrac{2\sqrt{34}}{5}\right)}=...\)
2 tháng 3 2022
Phương trình hoành độ giao điểm là:
\(x^2-x\sqrt{3}+\sqrt{3}-1=0\)
\(\text{Δ}=\left(\sqrt{3}\right)^2-4\cdot1\cdot\left(\sqrt{3}-1\right)=3-4\sqrt{3}+4=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{\sqrt{3}-2+\sqrt{3}}{2}=\sqrt{3}-1\\x_2=\dfrac{\sqrt{3}+2-\sqrt{3}}{2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_1=4-2\sqrt{3}\\y_2=1\end{matrix}\right.\)
27 tháng 5 2020
1. PT hoành độ giao điểm:
x2−(2x−m2+9)=0⇔x2−2x+m2−9=0(∗)
Khi m=1
thì pt trên trở thành: x2−2x−8=0
⇔(x−4)(x+2)=0⇒x=4
hoặc x=−2
Khi x=4⇒y=x2=16
. Giao điểm thứ nhất là (4,16)
Khi x=−2⇒y=x2=4
. Giao điểm thứ hai là (−2,4)
2. (P)
và (d) cắt nhau tại 2 điểm phân biệt ⇔(∗)
có 2 nghiệm phân biệt (hai nghiệm ấy chính là giá trị của 2 hoành độ giao điểm)
⇔Δ′=1−(m2−9)>0⇔10>m2(1)
Hai giao điểm nằm về phía của trục tung, nghĩa là 2 hoành độ giao điểm x1,x2
trái dấu. Điều này xảy ra khi x1x2<0⇔m2−9<0(2)
Từ (1);(2)
suy ra m2−9<0⇔−3<m<3
VL
25 tháng 5 2020
giúp mình đi vẽ hộ cái hình
cho đường tròn tâm O bán kính r,điểm A cố định nằm ngoài đường tròn.kẻ 2 tiếp tuyến AM,AN.Đường thẳng D đi qua A cắt đường tròn O tại B,C với AB<AC.Chứng minh 5 điểm A,M,N,O,I thuộc đường tròn
11 tháng 3 2021
a) Xét phương trình hoành độ giao điểm
\(x^2=-x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-2\Rightarrow y=4\end{matrix}\right.\)
Vậy tọa độ giao điểm là \(\left(1;1\right)\) và \(\left(-2;4\right)\)
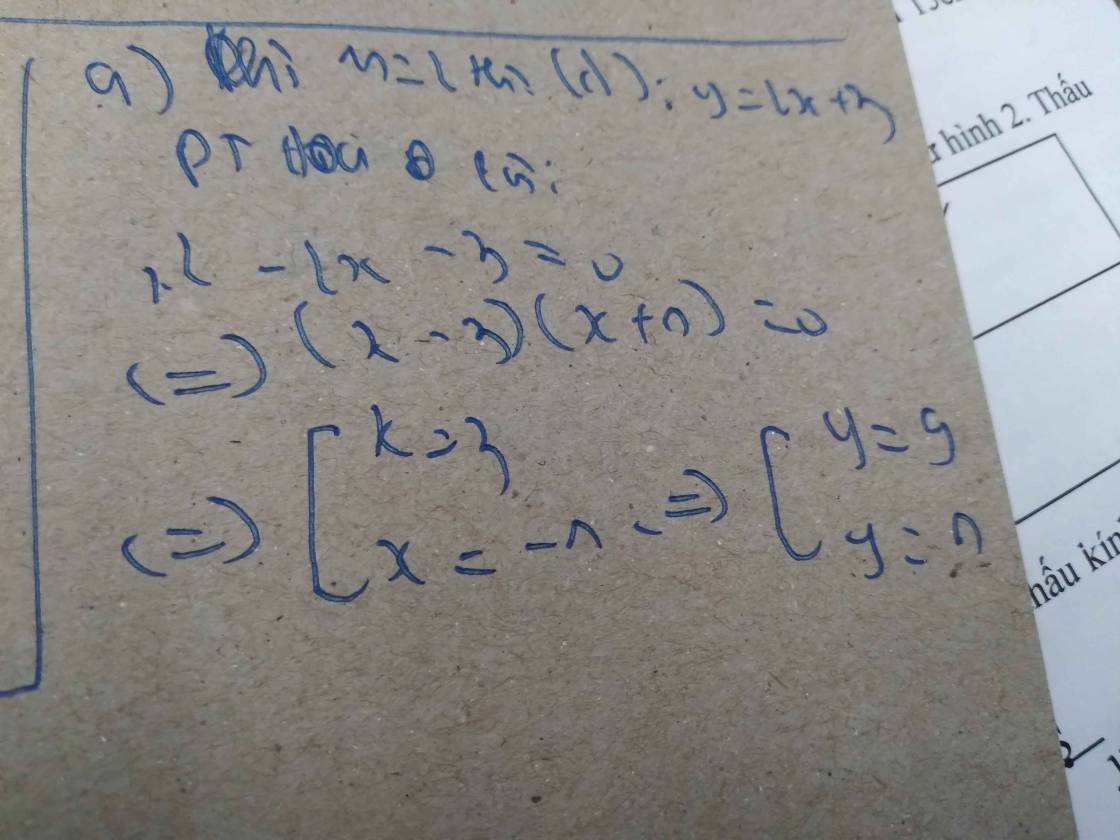
(P): y=-x^2
4x-5y=9
=>5y=4x-9
=>y=4/5x-9/5
PTHDGĐ là:
-x^2-4/5x+9/5=0
=>x=1 hoặc x=-9/5
=>y=1 hoặc y=81/25