Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tự
Giao điểm của (d1) và (d2):
$ 2x = -x + 3 \\\Leftrightarrow 3x = 3 \\\Leftrightarrow x = 1 \\\Leftrightarrow y = 2x = 2 . 1 = 2 $
Vậy giao điểm của (d1) và (d2) là $ (1;2) $
(d3) // (d1) $ \Rightarrow a = 2 $
(d3) cắt (d2) tại điểm có tung độ là 4
$ \Rightarrow \begin{case} 4 = -x + 3 \\ 4 = 2x + b \end{case} \\\Leftrightarrow x = -1 \Rightarrow b = 6 $

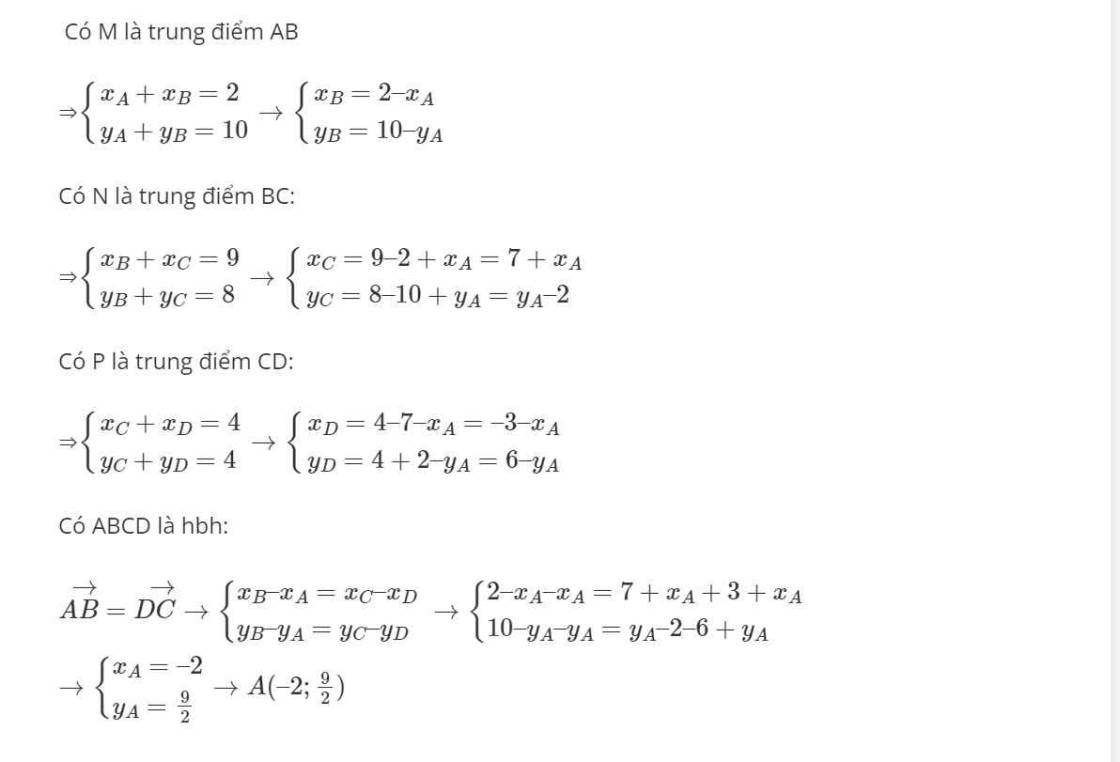
Tọa độ đỉnh B là:
\(\left\{{}\begin{matrix}x_B-2=2\\y_B+\dfrac{9}{2}=10\end{matrix}\right.\Leftrightarrow B\left(4;\dfrac{11}{2}\right)\)
Tọa độ đỉnh D là:
x=-3-(-2)=-1 và y=6-9/2=3/2
Tọa độ đỉnh C là:
x=7-2=5 và y=9/2-2=5/2

1) Trong he toa do Oxy, cho tam giac ABC co A(2;2), B(-5;3), C(-2;4). Goi H (x;y) la hinh chieu cua dinh A len duong thang BC. Tinh gia tri cua bieu thuc P = x2 + y2
Giải
- H là hình chiếu của A lên BC nên ta có: \(\overrightarrow{AH}.\overrightarrow{BC}=0\)
=> 3.(x-2) + 1.(y-2) = 0 <=> 3x + y =8 (1)
- H nằm trên đoạn BC nên : B,H,C thẳng hàng.
=> BH = kBC
=> \(\dfrac{x+5}{3}=\dfrac{y-3}{1}=x-3y=-14\)(2)
Từ (1) và (2) ta có hệ phương trình, giải hệ ta được: x=1, y=5.
Suy ra : x^2 + y^2 = 26 chọn B.


Bận ăn cơm :(
Bạn nhầm vị trí điểm I với điểm K à?
Vậy mình nêu hướng giải thôi nhé, làm biếng quá
Dễ dàng chứng minh \(\Delta_vADK=\Delta_vBAI\Rightarrow\widehat{DAK}=\widehat{IBA}\)
Mà \(\widehat{DAK}+\widehat{KAB}=90^0\Rightarrow\widehat{IBA}+\widehat{KAB}=90^0\Rightarrow AK\perp BI\)
Gọi E là trung điểm AB \(\Rightarrow CE//AK\) (hbh)
Gọi G là giao điểm BI và CE thì EG là đtb tam giác ABM (qua trung điểm E và song song cạnh đáy)
\(\Rightarrow\) G là trung điểm BM \(\Rightarrow CG\) là đường cao đồng thời là trung tuyến trong tam giác BCM
\(\Rightarrow\Delta BCM\) cân tại C \(\Rightarrow BC=CM=\sqrt{10}\)
\(AB=BC=\sqrt{10};AI=\frac{1}{2}AD=\frac{\sqrt{10}}{2}\)
\(\Rightarrow BI=\sqrt{AB^2+AI^2}=\frac{5\sqrt{2}}{2}\Rightarrow MB=\frac{AB^2}{BI}=2\sqrt{2}\)
\(\Rightarrow cos\widehat{MCB}=\frac{2BC^2-BM^2}{2BC^2}=\frac{3}{5}\)
\(\Rightarrow\) Viết được pt BC (qua C và tạo với đường thẳng CM đã biết 1 góc có \(cos=\frac{3}{5}\))
Tọa độ B là giao của BC và đường tròn tâm C bán kính BC có pt \(\left(x-2\right)^2+\left(y+2\right)^2=10\)
Nhân tiện hướng giải bài kia:
Gọi M là trung điểm AD, G là trọng tâm tam giác ABC
Do ABC cân tại A nên G và K cùng thuộc trung tuyến ứng với BC \(\Rightarrow GK\perp BC\)
E là trọng tâm ABD \(\Rightarrow\) DE đi qua trung điểm AB \(\Rightarrow\) DE là đường trung bình tam giác ABC (đi qua trung điểm của AB và AC)
\(\Rightarrow DE//BC\Rightarrow GK\perp DE\) (*)
K là tâm đường tròn ngoại tiếp, D là trung điểm AC \(\Rightarrow KD\perp AC\) (1)
G là trọng tâm ABC, E là trọng tâm ABD
\(\Rightarrow\left\{{}\begin{matrix}BG=\frac{2}{3}BD\\BE=\frac{2}{3}BM\end{matrix}\right.\) \(\Rightarrow EG//MD\) (Talet đảo) (2)
(1);(2) \(\Rightarrow KD\perp EG\) (**)
(*);(**) \(\Rightarrow\) G là trực tâm EDK \(\Rightarrow DG\perp EK\) hay \(BD\perp EK\)
\(\Rightarrow\) Viết được pt BD (qua Q và vuông góc EK)
Do D thuộc BD, gọi tọa độ D theo 1 ẩn
P thuộc AC \(\Rightarrow PD\perp KD\Rightarrow\overrightarrow{PD}.\overrightarrow{KD}=0\Rightarrow\) tìm được tọa độ D
Viết được pt AC (qua P và vuông góc BD)
Viết pt EG (qua E và song song AC) \(\Rightarrow\) tọa độ G là giao điểm EG và BD
\(\Rightarrow\) Phương trình GK \(\Rightarrow\) tọa đô A là giao GK và AC
\(\Rightarrow\)Tọa độ C (D là trung điểm AC)
\(\dfrac{-4^2+4\cdot1\cdot c}{4\cdot1}=\dfrac{5}{4}\)
\(\Leftrightarrow4\left(-16+4c\right)=20\)
\(\Leftrightarrow4c-16=5\)
hay \(c=\dfrac{21}{4}\)