Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B.
Với m = 0, phương trình 2 x 3 - 5 = 0 có nghiệm duy nhất.
Với m ≠ 0, đồ thị hàm số y = 2 x 3 + 3m x 2 - 5 chỉ cắt Ox tại một điểm khi y C Đ . y C T > 0. Ta có y' = 6 x 2 + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2 m 3 + 3 m 3 - 5 = m 3 - 5.
Suy ra y(0).y(-m) = -5(
m
3
- 5) > 0 ⇔ m < 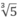

Đáp án: D.
Xét hàm số
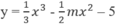
Ta có: y' = x 2 - mx = 0 ⇔ x = 0 hoặc x = 3
Nếu m = 0: Phương trình thành x 3 /3 - 5 = 0, có nghiệm duy nhất.
Nếu m ≠ 0: Phương trình đã cho có nghiệm duy nhất khi và chỉ khi cực đại và cực tiểu của hàm số
![]()
cùng dấu.
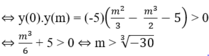

Lời giải:
Để hàm số đồng biến trên R thì:
\(y'=(m+2)x^2+2mx+1\geq 0\forall x\in\mathbb{R}\)
Theo định lý về dấu của tam thức bậc 2 thì điều này xảy ra khi :
\(\left\{\begin{matrix} m+2> 0\\ \Delta'=m^2-m-2\leq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m> -2\\ (m+1)(m-2)\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m> -2\\ -1\leq m\leq 2\end{matrix}\right.\)
\(\Leftrightarrow -1\leq m\leq 2\)
Đáp án B

Đáp án: B.
Hàm số đã cho có cực trị khi và chỉ khi
y' = 3 x 2 - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt
⇔ ∆ ' = m - 1 2 + (m + 3) = m 2 - m + 4 > 0
Ta thấy tam thức ∆ ' = m 2 - m + 4 luôn dương với mọi m vì
δ = 1 - 16 = -15 < 0, a = 1 > 0
Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R

Đáp án: B.
Hàm số đã cho có cực trị khi và chỉ khi
y' = 3 x 2 - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt
⇔ Δ' = ( m - 1 ) 2 + (m + 3) = m 2 - m + 4 > 0
Ta thấy tam thức Δ' = m 2 - m + 4 luôn dương với mọi m vì
δ = 1 - 16 = -15 < 0, a = 1 > 0
Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R




Đáp án: B.
Với m = 0, phương trình 2 x 3 - 5 = 0 có nghiệm duy nhất.
Với m ≠ 0, đồ thị hàm số y = 2 x 3 + 3m x 2 - 5 chỉ cắt Ox tại một điểm khi y CĐ . y CT > 0. Ta có y' = 6 x 2 + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2 m 3 + 3 m 3 - 5 = m 3 - 5.
Suy ra y(0).y(-m) = -5( m 3 - 5) > 0 ⇔ m < 5 3