Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khi \(m=0\Rightarrow y=x-1\) nên hàm số không có cực trị
- Khi \(m\ne0\Rightarrow y'=3mx^2+6mx-\left(m-1\right)\)
hàm số không có cực trị khi và chỉ chỉ y' = 0 không có nghiệm hoặc có nghiệm kép
\(\Leftrightarrow\Delta'=9m^2+3m\left(m-1\right)=12m^2-3m\le0\) \(\Leftrightarrow0\le m\)\(\le\frac{1}{4}\)

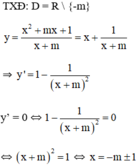
Ta có bảng biến thiên:
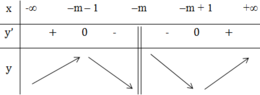
Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.
Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.
Vậy m = -3.

Tập xác định :
Nếu hàm số đạt cực đại tại x = 2 thì y'(2) = 0 ⇔ m2 + 4m + 3 = 0 ⇔ m=-1 hoặc m=-3
- Với m = -1, ta có :
x=0 hoặc x=2.
Ta có bảng biến thiên :
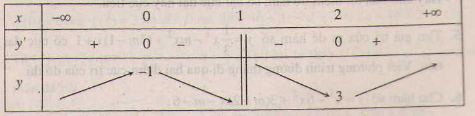
Trường hợp này ta thấy hàm số không đạt cực đại tại x = 2.
- Với m = -3, ta có:
x=2 hoặc x=4
Ta có bản biến thiên :
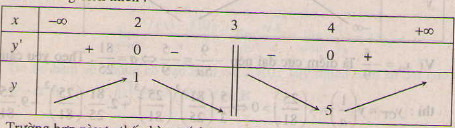
Trường hợp này ta thấy hàm số đạt cực đại tại x = 2.
Vậy m = -3 là giá trị cần tìm.

Lời giải + diễn giải
để hàm có cực trị f'(x) phải có nghiệm và đổi dấu qua nghiệm
a) \(y'=3x^2-6x+m\)
xét f(x)= 3x^2 -6x+m
để f(x) là hàm bậc 2 => có nghiệm và đổi dấu qua nghiệm đk cần và đủ \(\Delta>0\)
\(\Leftrightarrow\Delta'=9-3m>0\Rightarrow m< 3\)
Kết luận với m< 3 hàm A(x) luôn có cực trị
b)
\(y'=3x^2+4mx+m\)
\(\Delta'=4m^2-3m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>\dfrac{3}{4}\end{matrix}\right.\)
c)
\(y=\dfrac{x^2-2mx+5}{x-m}\Rightarrow\left\{{}\begin{matrix}x\ne m\\y=\left(x-m\right)+\dfrac{5-m^2}{x-m}\end{matrix}\right.\)
\(y'=1+\dfrac{m^2-5}{\left(x-m\right)^2}\)
\(y'=0\Leftrightarrow\left(x-m\right)^2+m^2-5=0\Rightarrow5-m^2>0\Rightarrow-\sqrt{5}< m< \sqrt{5}\)

\(y'=3x^2-4x+m\)
Để hàm số đạt cực tiểu tai x = 1 thì x = 1 là nghiệm của y' và y' đổi dấu khi đi qua x = 1.
Để x = 1 là nghiệm của y' thì:
\(3.1^2-4.1+m=0\) \(\Rightarrow m=1\)
Với m = 1. khi đó: \(y'=3x^2-4x+1\) có 2 nghiệm là \(1\) và \(\dfrac{1}{3}\); \(y'\) đổi dấu từ âm sang dương khi đi qua x = 1. Vậy hàm số có cực tiểu tại x = 1.

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 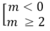

Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 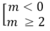

TXĐ: D = R
y’ = 3 x 2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 x 2 + 4mx + m có hai nghiệm phân biệt.
⇔ Δ’ = 4 m 2 -3m > 0 ⇔ m(4m – 3) > 0
⇔ 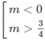
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.

TXĐ: D = R
y’ = 3 x 2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3 x 2 + 4mx + m có hai nghiệm phân biệt.
⇔ ∆ ’ = 4 m 2 -3m > 0 ⇔ m(4m – 3) > 0
⇔ 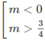
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc m > 3/4.
Hàm số không có cực trị khi đạo hàm của nó không đổi dấu trên tập xác định R\{m}.
Ta có:
Xét g(x) = x 2 – 2mx – 2 m 2 + 3
∆ ’g = m 2 + 2 m 2 – 3 = 3( m 2 – 1) ;
∆ ’g ≤ 0 khi – 1 ≤ m ≤ 1.
Khi – 1 ≤ m ≤ 1 thì phương trình g(x) = 0 vô nghiệm hay y’ = 0 vô nghiệm và y’ > 0 trên
tập xác định. Khi đó, hàm số không có cực trị.
Khi m = 1 hoặc m = -1, hàm số đã cho trở thành y = x + 3 (với x ≠ 1) hoặc y = x – 3 (với x ≠ - 1) Các hàm số này không có cực trị.
Vậy hàm số đã cho không có cực trị khi – 1 ≤ m ≤ 1.