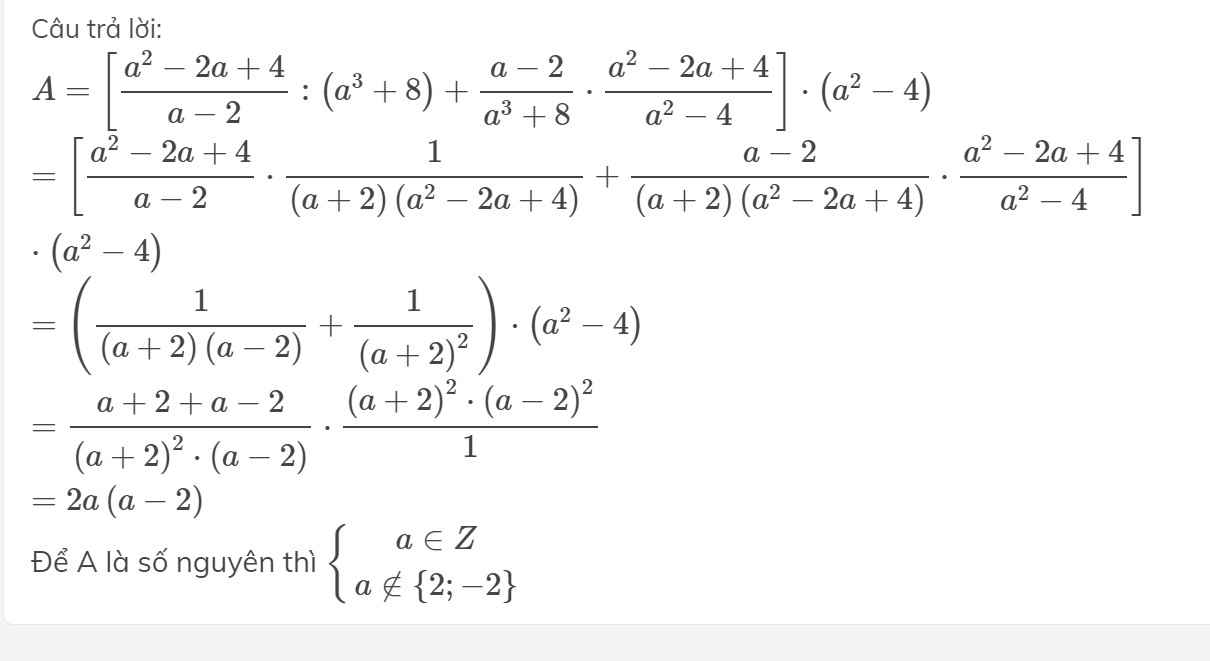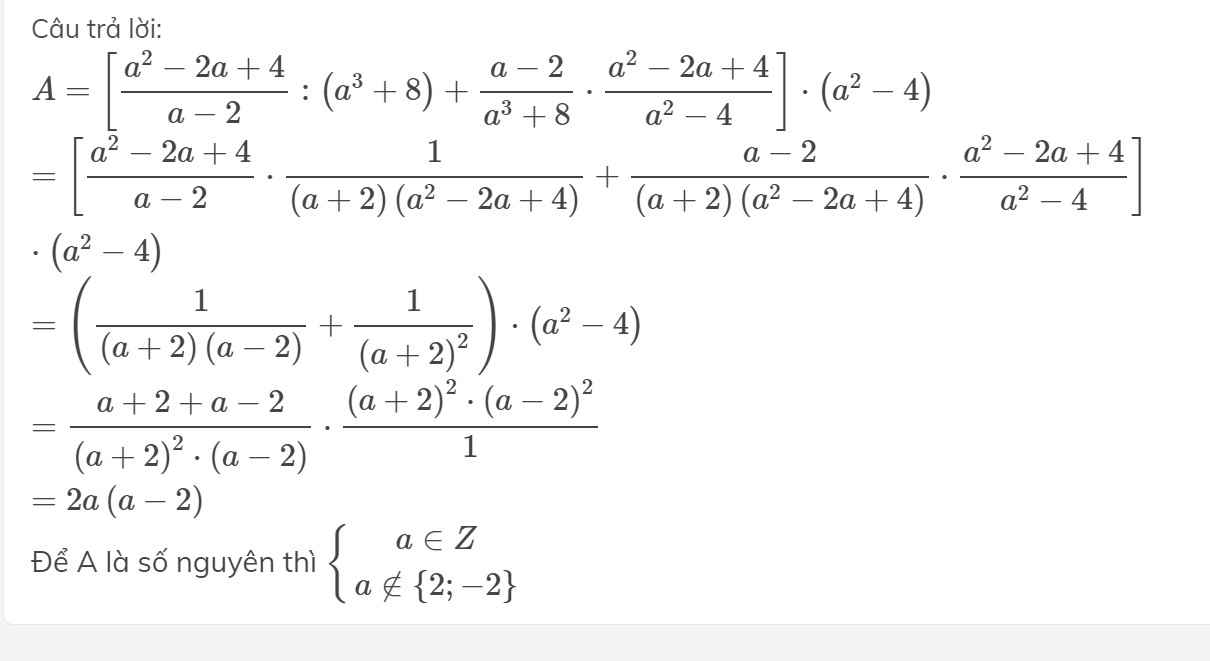
\(\left[\dfrac{a^2-2...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a, \(\dfrac{x^2-x}{x-2}+\dfrac{4-3x}{x-2}\) \(=\dfrac{x^2-x+4-3x}{x-2}=\dfrac{x^2-4x+4}{x-2}\) c) \(\dfrac{2}{x^2-9}+\dfrac{1}{x+3}\) Ta có: \(\dfrac{1}{x+3}=\dfrac{1\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{x-3}{x^2-9}\) \(\Rightarrow\dfrac{2}{x^2-9}+\dfrac{1}{x+3}=\dfrac{2}{x^2-9}+\dfrac{x-3}{x^2-9}=\dfrac{2+x-3}{x^2-9}=\dfrac{x-1}{x^2-9}\) Câu 1: Ta có: \(\left(\dfrac{a+b}{2}\right)^2\ge ab\) \(\Leftrightarrow\dfrac{\left(a+b\right)^2}{2^2}-ab\ge0\) \(\Leftrightarrow\dfrac{a^2+2ab+b^2-4ab}{4}\ge0\) \(\Leftrightarrow\dfrac{a^2-2ab+b^2}{4}\ge0\) \(\Leftrightarrow\dfrac{\left(a-b\right)^2}{4}\ge0\) Vì \(\left(a-b\right)^2\ge0\forall a,b\) \(\Rightarrow\dfrac{\left(a-b\right)^2}{4}\ge0\forall a,b\) \(\Rightarrow\left(\dfrac{a+b}{2}\right)^2\ge ab\) (1) Ta có: \(\dfrac{a^2+b^2}{2}\ge\left(\dfrac{a+b}{2}\right)^2\) \(\Leftrightarrow\dfrac{a^2+b^2}{2}-\dfrac{\left(a+b\right)^2}{4}\ge0\) \(\Leftrightarrow\dfrac{2a^2-2b^2-a^2-2ab-b^2}{4}\ge0\) \(\Leftrightarrow\dfrac{a^2-2ab-b^2}{4}\ge0\) \(\Leftrightarrow\dfrac{\left(a-b\right)^2}{4}\ge0\) Vì \(\left(a-b\right)^2\ge0\forall a,b\) \(\Rightarrow\dfrac{\left(a-b\right)^2}{4}\ge0\forall a,b\) \(\Rightarrow\dfrac{a^2+b^2}{2}\ge\left(\dfrac{a+b}{2}\right)^2\) (2) Từ (1) và (2) \(\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2\le\dfrac{a^2+b^2}{2}\) 5 , a3+b3+c3\(\ge\) 3abc \(\Leftrightarrow\) a3+3a2b+3ab2+b3+c3-3a2b-3ab2-3abc\(\ge\) 0 \(\Leftrightarrow\) (a+b)3+c3-3ab(a+b+c) \(\ge0\) \(\Leftrightarrow\) (a+b+c)(a2+2ab+b2-ac-bc+c2)-3ab(a+b+c) \(\ge0\) \(\Leftrightarrow\) (a+b+c)(a2+b2+c2-ab-bc-ca)\(\ge0\) (1) ta co : a,b,c>0 \(\Rightarrow\)a+b+c>0 (2) (a-b)2+(b-c)2+(c-a)2\(\ge0\) <=> 2a2+2b2+2c2-2ac-2cb-2ab\(\ge0\) <=>a2+b2+c2-ab-bc-ac\(\ge\) 0 (3) Từ (1)(2)(3)=> pt luôn đúng 1: \(\Leftrightarrow\left(x+2\right)\left(x-2\right)+3\left(x+1\right)=3+x^2-x-2\) \(\Leftrightarrow x^2-x+1=x^2-4+3x+3=x^2+3x-1\) =>-4x=-2 hay x=1/2 2: \(\Leftrightarrow\left(x+6\right)^2+\left(x-5\right)^2=2x^2+23x+61\) \(\Leftrightarrow x^2+12x+36+x^2-10x+25=2x^2+23x+61\) \(\Leftrightarrow2x^2+23x+61=2x^2+2x+11\) =>21x=-50 hay x=-50/21 3: \(\Leftrightarrow6\left(x-8\right)+\left(x+2\right)\left(x-5\right)=-18-\left(x-5\right)\left(x-8\right)\) \(\Leftrightarrow6x-48+x^2-3x-10+18+x^2-13x+40=0\) \(\Leftrightarrow2x^2-10x=0\) =>2x(x-5)=0 =>x=0(nhận) hoặc x=5(loại) B1: \(ab+bc+ca\le a^2+b^2+c^2< 2\left(ab+bc+ca\right)\) Xét hiệu: \(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca\) \(=\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(a^2-2ac+c^2\right)\) \(=\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\) => BĐT luôn đúng * Ta có: \(a< b+c\Rightarrow a^2< ab+ac\) \(b< a+c\Rightarrow b^2< ab+ac\) \(c< a+b\Rightarrow a^2< ac+bc\) Cộng từng vế bất đẳng thức ta được: \(a^2+b^2+c^2< 2\left(ab+bc+ca\right)\) Vậy: \(ab+bc+ca\le a^2+b^2+c^2< 2\left(ab+bc+ca\right)\) B2: Ta có: \(a+b>c\) ; \(b+c>a\); \(a+c>b\) Xét:\(\dfrac{1}{a+c}+\dfrac{1}{b+c}>\dfrac{1}{a+b+c}+\dfrac{1}{b+c+a}=\dfrac{2}{a+b+c}>\dfrac{2}{a+b+a+b}=\dfrac{1}{a+b}\) \(\dfrac{1}{a+b}+\dfrac{1}{a+c}>\dfrac{1}{a+b+c}+\dfrac{1}{a+c+b}=\dfrac{2}{a+b+c}>\dfrac{2}{b+c+b+c}=\dfrac{1}{b+c}\) \(\dfrac{1}{a+b}+\dfrac{1}{b+c}>\dfrac{1}{a+b+c}+\dfrac{1}{b+c+a}=\dfrac{2}{a+b+c}>\dfrac{2}{a+c+a+c}=\dfrac{1}{a+c}\) Suy ra: \(\dfrac{1}{a+c}+\dfrac{1}{b+c}>\dfrac{1}{a+b}\) \(\dfrac{1}{a+b}+\dfrac{1}{a+c}>\dfrac{1}{b+c}\) \(\dfrac{1}{a+b}+\dfrac{1}{b+c}>\dfrac{1}{a+c}\) => ĐPCM a) \(N=8a^3-27b^3\) \(=\left(2a\right)^3-\left(3b\right)^3\) \(=\left(2a-3b\right)^3+18ab\left(2a-3b\right)\) \(=5^3+18\cdot12\cdot5\) \(=125+1080=1205\) b) \(K=a^3+b^3+6a^2b^2\left(a+b\right)+3ab\left(a^2+b^2\right)\) \(=a^3+b^3+6a^2b^2+3a^3b+3ab^3\) \(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\left(a^2+2ab+b^2\right)\) \(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\left(a+b\right)^2\) \(=\left(a+b\right)^3+3ab\left(a+b\right)\left(a+b-1\right)\) \(=1^3+3ab\cdot1\cdot0\) \(=1\) a ) \(N=8a^3-27b^3\) \(\Leftrightarrow N=\left(2a-3b\right)\left(4x^2+6ab+9b^2\right)\) \(\Leftrightarrow N=5\left(4x^2+9b^2+72\right)\) Ta có : \(2a-3b=5\) \(\Leftrightarrow4a^2+9b^2=25+6ab\) Thay vào ta được : \(N=5\left(25+6ab+72\right)=845\) b ) \(K=a^3+b^3+6a^2b^2\left(a+b\right)+3ab\left(a^2+b^2\right)\) \(\Leftrightarrow K=\left(a+b\right)^3-3ab\left(a+b\right)+6a^2b^2\left(a+b\right)+3ab\left(a+b\right)^2-6a^2b^2\) \(\Leftrightarrow K=1-3ab+6a^2b^2+3ab-6a^2b^2=1\) c ) \(P=\left(\dfrac{x}{4}\right)^3+\left(\dfrac{y}{2}\right)^3\) \(\Leftrightarrow P=\left(\dfrac{x}{4}+\dfrac{y}{2}\right)^3-3\left[\left(\dfrac{x}{4}\right)^2\dfrac{y}{2}+\dfrac{x}{4}\left(\dfrac{y}{2}\right)^2\right]\) \(\Leftrightarrow P=\left(\dfrac{2\left(x+2y\right)}{8}\right)^3-3\left[\dfrac{x^2y}{32}+\dfrac{xy^2}{16}\right]\) \(\Leftrightarrow P=8-3xy\left(\dfrac{x+2y}{32}\right)\) \(\Leftrightarrow P=8-3.4\left(\dfrac{8}{32}\right)=5\) \(1.\) \(a.\) \(\dfrac{8}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{2}{x^2+3}+\dfrac{1}{x+1}\) \(=\dfrac{8}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{2\left(x^2-1\right)}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{1\left(x-1\right)\left(x^2+3\right)}{\left(x^2-1\right)\left(x^2+3\right)}\) \(=\dfrac{8}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{2x^2-2}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{x^3-x^2+3x-3}{\left(x^2-1\right)\left(x^2+3\right)}\) \(=\dfrac{8+2x^2-2+x^3-x^2+3x-3}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=\dfrac{x^3+x^2+3x+3}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=\dfrac{x^2\left(x+1\right)+3\left(x+1\right)}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=\dfrac{\left(x^2+3\right)\left(x+1\right)}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=x-1\) \(b.\) \(\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{2y^2}{x^2-y^2}\) \(=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{2y^2}{\left(x-y\right)\left(x+y\right)}\) \(=\dfrac{\left(x+y\right)^2}{2\left(x^2-y^2\right)}-\dfrac{\left(x-y\right)^2}{2\left(x^2-y^2\right)}+\dfrac{4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{x^2+2xy+y^2}{2\left(x^2-y^2\right)}-\dfrac{x^2-2xy+y^2}{2\left(x^2-y^2\right)}+\dfrac{4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{4xy+4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{4y\left(x+y\right)}{2\left(x^2-y^2\right)}\) \(=\dfrac{2y}{\left(x-y\right)}\) Tương tự các câu còn lại
K
Khách
NL
Nguyễn Lê Phước Thịnh
27 tháng 5 2022
Đúng(1)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 11 2018
19 tháng 11 2018
23 tháng 3 2018
AW
23 tháng 3 2018
5 tháng 6 2022
ND
3 tháng 4 2018
ND
3 tháng 4 2018
N
28 tháng 6 2018
28 tháng 6 2018
8 tháng 12 2017
