VN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LV
18 tháng 1 2022
một đòn bẫy dài một mét .đặt ở đâu để có thể dùng 3600n có thể nâng tảng đá nặng 120kg?
3 tháng 7 2022
a: \(\dfrac{1}{x-2}+3=\dfrac{3-x}{x-2}\)
=>1+3x-6=3-x
=>3x-5=3-x
=>4x=8
hay x=2(loại)
b: \(\Leftrightarrow8-x-8\left(x-7\right)=-26\)
=>8-x-8x+56=-26
=>-9x+64=-26
=>-9x=-90
hay x=10(nhận)
c: \(\dfrac{1}{x-2}+\dfrac{1}{x-3}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\dfrac{x-3+x-2}{\left(x-2\right)\left(x-3\right)}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\left(x-1\right)\left(2x-5\right)=2\left(x^2-5x+6\right)\)
\(\Leftrightarrow2x^2-5x-2x+5=2x^2-10x+12\)
=>-7x+10x=12-5
=>3x=7
hay x=7/3(nhận)
23 tháng 5 2022
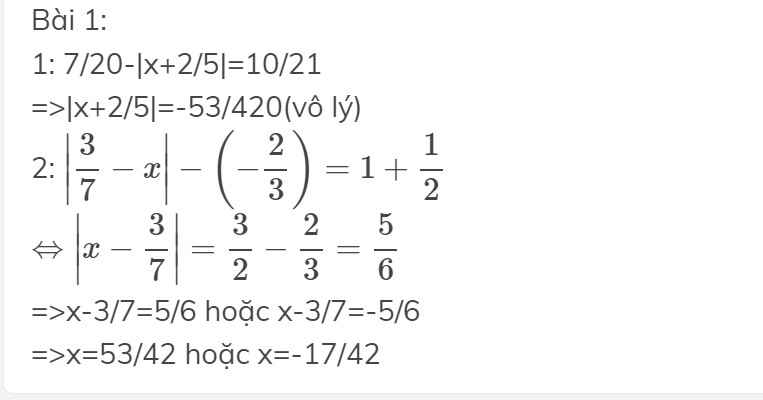
3: \(-\dfrac{1}{2}+\left|\dfrac{1}{3}x+\dfrac{2}{5}\right|=\dfrac{5}{7}\cdot\dfrac{3}{11}+\dfrac{8}{11}\cdot\dfrac{5}{7}=\dfrac{5}{7}\)
=>|1/3x+2/5|=5/7+1/2=17/14
=>1/3x+2/5=17/14 hoặc 1/3x+2/5=-17/14
=>x=171/70 hoặc x=-339/70
MT
20 tháng 6 2015
(x+1)(x-1)+(x+2)(x-2)+(x+3)(x-3)+(x+4)(x-4)+(x+5)(x-5)+(x+6)(x-6)+(x+7)(x-7)+(x+8)(x-8)
=x2-1+x2-4+x2-9+x2-16+x2-25+x2-36+x2-49+x2-64
=8x2-204
rút gọn à
21 tháng 9 2020
P/S : Câu 2,3 kết quả bằng bao nhiêu mới tìm được x ?
1.\(\left(2x-7\right)^2-4\left(x-3\right)=5\)
=> \(\left(2x\right)^2-2\cdot2x\cdot7+7^2-4x+12=5\)
=> \(4x^2-28x+49-4x+12=5\)
=> \(4x^2-32x+61=5\)
=> \(4x^2-32x+61-5=0\)
=> \(4x^2-32x+56=0\)
=> \(4\left(x^2-8x+14\right)=0\)
=> \(x^2-8x+14=0\)
=> \(\orbr{\begin{cases}x=4-\sqrt{2}\\x=\sqrt{2}+4\end{cases}}\)
4.\(\left(3x-1\right)^2-6\left(x-1\right)\left(x+1\right)-3x\left(x-2\right)=7\)
=> \(\left(3x\right)^2-2\cdot3x\cdot1+1^2-6\left(x^2-1\right)-3x^2+6x=7\)
=> \(9x^2-6x+1-6x^2+6-3x^2+6x=7\)
=> \(\left(9x^2-6x^2-3x^2\right)+\left(-6x+6x\right)+\left(1+6\right)=7\)
=> 7 = 7(đúng)
5. \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\)
=> \(x^2+2\cdot x\cdot3+3^2-x\left(x+8\right)+4\left(x+8\right)=1\)
=> x2 + 6x + 9 - x2 - 8x + 4x + 32 = 1
=> (x2 - x2) + (6x - 8x + 4x) + (9 + 32) = 1
=> 2x + 41 = 1
=> 2x = -40
=> x = -20
\(x^7+x^2+1\)
\(=x^7+x^6+x^5-x^6-x^5-x^4+x^4+x^3+x^2-x^3-x^2-x+x^2+x+1\)
\(=x^5\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^2\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)
\(x^7+x^5+1\)
\(=x^7-x^6+x^5-x^3+x^2+x^6-x^5+x^4-x^2+x+x^5-x^4+x^3-x+1\)
\(=x^2\left(x^5-x^4+x^3-x+1\right)+x\left(x^5-x^4+x^3-x+1\right)+\left(x^5-x^4+x^3-x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^5-x^4+x^3-x+1\right)\)
\(x^8+x^2+1>0\) \(\forall x\)
=> ko thể phân tích thành nhân tử