K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VK
1
YN
27 tháng 4 2022
a)
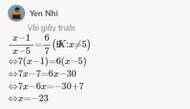
b) \(\dfrac{x^2}{6}=\dfrac{24}{25}\)
\(\Leftrightarrow\left(5x\right)^2=144\)
\(\Leftrightarrow\left(5x\right)^2=12^2\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=12\\5x=-12\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{12}{5}\\x=-\dfrac{12}{5}\end{matrix}\right.\)
c) \(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
\(\Leftrightarrow\left(x-2\right)\left(x+7\right)=\left(x-1\right)\left(x+4\right)\)
\(\Leftrightarrow x^2+5x-14=x^2+3x-4\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9 2024
Bài 1:
a; \(\dfrac{7}{8}\) + \(x\) = \(\dfrac{4}{7}\)
\(x\) = \(\dfrac{4}{7}\) - \(\dfrac{7}{8}\)
\(x\) = \(\dfrac{32}{56}\) - \(\dfrac{49}{56}\)
\(x=-\) \(\dfrac{49}{56}\)
Vậy \(x=-\dfrac{49}{56}\)
b; 6 - \(x\) = - \(\dfrac{3}{4}\)
\(x\) = 6 + \(\dfrac{3}{4}\)
\(x\) = \(\dfrac{24}{4}+\dfrac{3}{4}\)
\(x=\dfrac{27}{4}\)
Vậy \(x=\dfrac{27}{4}\)
c; \(\dfrac{1}{-5}\) + \(x\) = \(\dfrac{3}{4}\)
\(x\) = \(\dfrac{3}{4}\) + \(\dfrac{1}{5}\)
\(x=\dfrac{15}{20}\) + \(\dfrac{4}{20}\)
\(x=\dfrac{19}{20}\)
Vậy \(x=\dfrac{19}{20}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9 2024
Bài 1:
d; - 6 - \(x\) = - \(\dfrac{3}{5}\)
\(x\) = - 6 + \(\dfrac{3}{5}\)
\(x=-\dfrac{30}{5}\) + \(\dfrac{3}{5}\)
\(x=-\dfrac{27}{5}\)
Vậy \(x=-\dfrac{27}{5}\)
e; - \(\dfrac{2}{6}\) + \(x\) = \(\dfrac{5}{7}\)
\(x\) = \(\dfrac{5}{7}\) + \(\dfrac{2}{6}\)
\(x\) = \(\dfrac{15}{21}\) + \(\dfrac{1}{3}\)
\(x=\dfrac{15}{21}\) + \(\dfrac{7}{21}\)
\(x=\dfrac{22}{21}\)
Vậy \(x=\dfrac{22}{21}\)
f; - 8 - \(x\) = - \(\dfrac{5}{3}\)
\(x\) = \(-\dfrac{5}{3}\) + 8
\(x\) = \(\dfrac{-5}{3}\) + \(\dfrac{24}{3}\)
\(x\) = \(\dfrac{-19}{3}\)
Vậy \(x=-\dfrac{19}{3}\)
4 tháng 7 2016
1) \(\frac{17}{6}-\left(x-\frac{7}{6}\right)=\frac{7}{4}\)
\(\Rightarrow x-\frac{7}{6}=\frac{17}{6}-\frac{7}{4}\)
\(\Rightarrow x=\frac{13}{12}+\frac{7}{6}=\frac{9}{4}\)
2) \(\frac{3}{35}-\left(\frac{3}{5}-x\right)=\frac{2}{7}\)
\(\Rightarrow\)\(\frac{3}{5}-x=\frac{3}{35}-\frac{2}{7}=-\frac{1}{5}\)
\(\Rightarrow x=\frac{3}{5}-\left(-\frac{1}{5}\right)=\frac{4}{5}\)
3) 4) Hjhj^_^^_^
28 tháng 5 2022
1: Trường hợp 1: x<-2
Pt sẽ là -x-2+5-x=7
=>-2x+3=7
=>-2x=4
hay x=-2(loại)
Trường hợp 2: -2<=x<5
Pt sẽlà x+2+5-x=7
=>7=7(luôn đúng)
Trường hợp 3: x>=5
Pt sẽ là x+2+x-5=7
=>2x-3=7
=>x=5(nhận)
4: \(\left|x^2-2x\right|=x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=0\\\left(x^2-2x\right)^2=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x^2-2x-x\right)\left(x^2-2x+x\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x^2-3x\right)\left(x^2-x\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{0;1;3\right\}\)
5: Ta có: \(\left|2x+3\right|=x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-2\\\left(2x+3+x+2\right)\left(2x+3-x-2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-2\\\left(3x+5\right)\left(x+1\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{-\dfrac{5}{3};-1\right\}\)
6: |5x-4|=|x+2|
=>5x-4=x+2 hoặc 5x-4=-x-2
=>4x=6 hoặc 6x=2
=>x=3/2 hoặc x=1/3
15 tháng 5 2017
a) Thu gọn, sắp xếp các đa thức theo lũy thừa tăng của biến
f(x)=x2+2x3−7x5−9−6x7+x3+x2+x5−4x2+3x7
= -9 - 2x2 + 3x3 - 6x5 - 3x7
g(x)=x5+2x3−5x8−x7+x3+4x2−5x7+x4−4x2−x6−12
= -12 + 3x3 + x4 + x5 - x6 - 6x7 - 5x8
h(x)=x+4x5−5x6−x7+4x3+x2−2x7+x6−4x2−7x7+x
= 2x - 3x2 + 4x3 +4x5 -4x6 - 10x7
b) Tính f(x) + g(x) − h(x) = ( -9 - 2x2 + 3x3 - 6x5 - 3x7 ) + (-12 + 3x3 + x4 + x5 - x6 - 6x7 - 5x8 ) - (2x - 3x2 + 4x3 +4x5 -4x6 - 10x7)
= - 9 - 2x2 + 3x3 - 6x5 - 3x7 -12 + 3x3 + x4 + x5 - x6 - 6x7 - 5x8 - 2x + 3x2 - 4x3 - 4x5 + 4x6 + 10x7
= -21 - 2x + x2 + 2x3 + x4 - 9x5 + 3x6 + x7 - 5x8
3 tháng 4 2019
ta có h(x)=\(\left(-8x^3+8x^3\right)+\left(3x^7-x^7-2x^7\right)+x^4-36+49\)
(=)h(x)=\(x^4+13\)
=>\(x^4+13=1\left(=\right)x^4=-12\)=> ko tồn tại x thỏa mãn
ta có \(x^4\ge0\)=>\(x^4+13\ge13>0\)
Vậy h(x)luôn nhận giá trị dương
KN
1
LN
17 tháng 7 2015
a) |2+x|+|x-7|=3
Ta có: 2+x=0=>x=-2
x-7=0=>x=7
Lập bảng xét dấu:
x -2 7
2+x - 0 + +
x-7 - - 0 +
Nếu x<-2 thì: |2+x|= -(2+x)=-2-x
|x-7|=-(x-7)=-x+7
Khi đó: (-2-x)+(-x+7)=3
=> -2-x-x-7=3
=> -x-x=3+2+7
=> -2x= 12
=> x= -6( thỏa mãn x<-2)
Nếu -2\(\le\)x\(\le\)7 thì: |2+x|=2+x
|x-7|=-(x-7)=-x+7
Khi đó: (2+x)+(-x+7)=3
=> 2+x-x+7=3
=> +x-x=3-2-7
=> 0= -6 (Vô lý)
Nếu x>7 thì: |2+x|=2+x
|x-7|=x-7
Khi đó; (2+x)+(x-7)=3
=> 2+x+x+7=3
=> x+x=3-2-7
=> 2x=-6
=> x= -3( không thỏa mãn x>7)
Vậy x= -6
\(x^2\left(x-7\right)-6\left(7-x\right)\)
\(=x^2\left(-7+x\right)-6\left(7-x\right)\)
\(=-x^2\left(7-x\right)-6\left(7-x\right)\)
\(=\left(-x^2-6\right)\left(7-x\right)\)