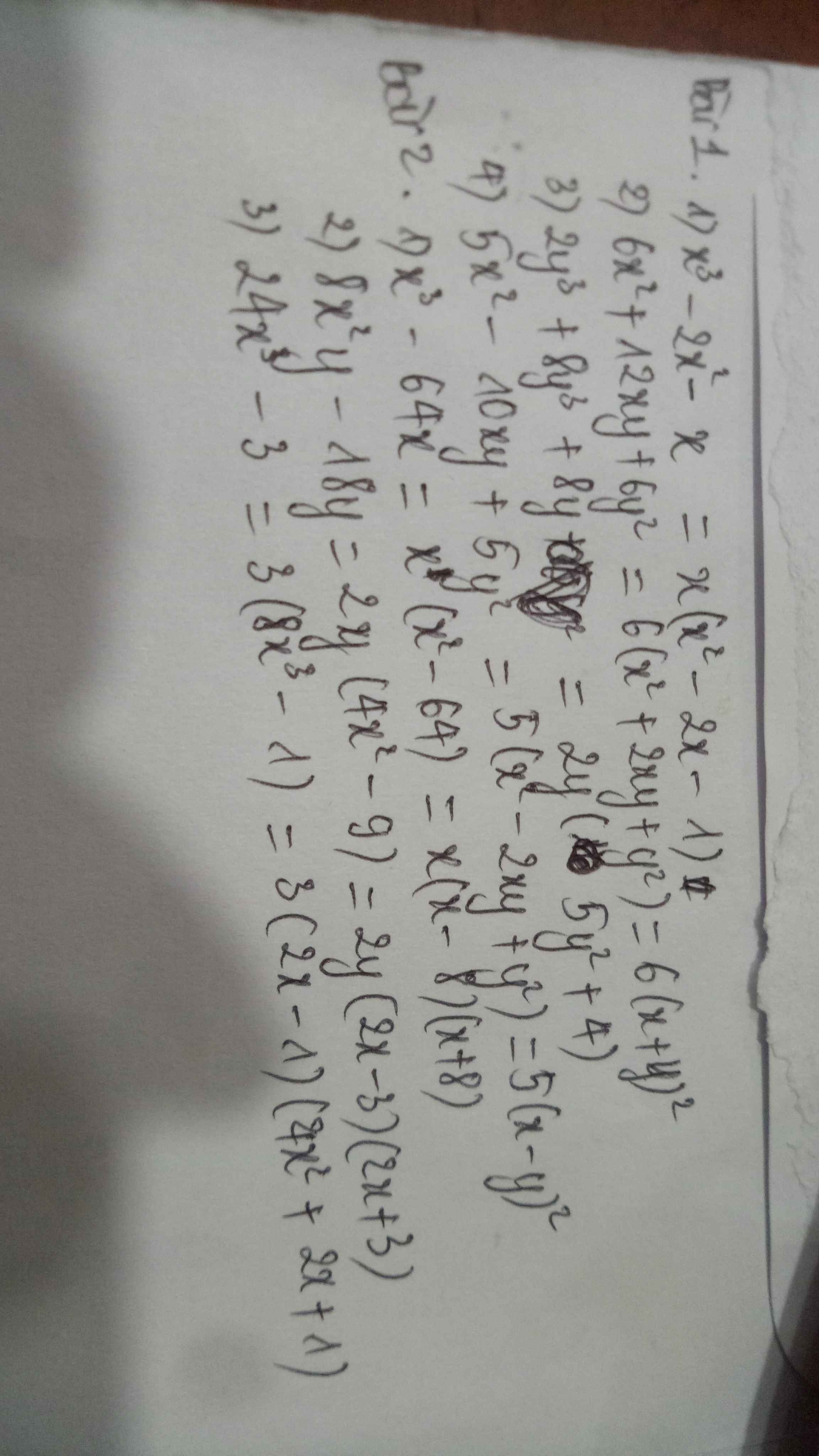Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a) x2 + 4x + 3
= x2 + 3x + x +3
= ( x2 + 3 ) + ( x + 3 )
= x ( x + 3 ) + ( x + 3 )
= ( x + 3 ) ( x + 1 )
b) 4x2 - 4x - 3
= 4x2 + 2x - 6x - 3
= ( 4x2 + 2x ) - ( 6x + 3 )
= 2x ( 2x + 1 ) - 3 ( 2x + 1 )
= ( 2x + 1 )( 2x - 3 )
c) x2 - x - 12
= x2 + 3x - 4x - 12
= ( x2 + 3x ) - ( 4x + 12 )
= x ( x + 3 ) - 4 ( x + 3 )
= ( x + 3 ) ( x - 4 )
d) 4x4 - 4x2y2 - 8y4
= 4 ( x4 - x2y2 - 2y4 )
Hk tốt

a. Đặt \(x^2-2y=a\)
ta có : \(\left(x^2-2y\right)^2-4\left(x^2-2y\right)-12=a^2-4a-12=a^2-6a+2a-12=\left(a-6\right)\left(a+2\right)\)
\(=\left(x^2-2y-6\right)\left(x^2-2y+2\right)\)
b. Đặt \(x+6=a\Rightarrow\left(x+3\right)\left(x+6\right)\left(x+9\right)+45=\left(a-3\right)a\left(a+3\right)+45\)
\(=a^3-9a+45\) nghiệm xấu quá không nhóm được ban ơi :((

Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)

x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung

a) \(x^2-2x-4y^2-4y=\left(x^2-2x+1\right)-\left(4y^2+4y+1\right)\)
\(=\left(x-1\right)^2-\left(2y+1\right)^2=\left(x-1-2y-1\right)\left(x-1+2y+1\right)\)
\(=\left(x-2y-3\right)\left(x+2y\right)\)
b) \(x^2-4x^2y^2+y^2+2xy=\left(x^2+2xy+y^2\right)-4x^2y^2\)
\(=\left(x+y\right)^2-4x^2y^2=\left(x+y-2xy\right)\left(x+y+2xy\right)\)
c) \(x^6-x^4+2x^3+2x^2=\left(x^6+2x^3+1\right)-\left(x^4-2x^2+1\right)\)
\(=\left(x^3+1\right)^2-\left(x^2-1\right)^2=\left(x^3+1-x^2+1\right)\left(x^3+1+x^2-1\right)=x^2\left(x^3-x^2+2\right)\left(x+1\right)\)
d) \(x^3+3x^2+3x+1-8y^3=\left(x+1\right)^3-8y^3=\left(x+1-2y\right)\left(x^2+2x+1+2xy+2y+4y^2\right)\)