Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=x^{64}-1-x^{64}\)
\(C=-1\)
Vậy gtri của C không phụ thuộc vào x

\(B=\left(x-3\right)^2+\left(x-11\right)^2\)
\(=x^2-6x+9+x^2-22x+121\)
\(=2\left(x^2-14x+49\right)+32\)
\(=2\left(x-7\right)^2+32\)
Ta có: \(\left(x-7\right)^2\ge0\Leftrightarrow2\left(x-7\right)^2+32\ge32\)
Vậy \(MinB=32\Leftrightarrow x=7\)
\(C=\left(x+1\right)\left(x-2\right)\left(x-3\right)\left(x-6\right)\)
\(=\left(x+1\right)\left(x-6\right)\left(x-2\right)\left(x-3\right)\)
\(=\left(x^2-5x-6\right)\left(x^2-5x+6\right)\)
Đặt \(c=x^2-5x\)lúc này \(C\)thành: \(C=\left(c-6\right)\left(c+6\right)=c^2-36\)
Mà: \(c^2\ge0\forall c\Leftrightarrow c^2-36\ge-36\Leftrightarrow C\ge-36\)
Dấu '' = '' xảy ra: \(c=0\)
\(\Leftrightarrow x^2-5x=0\)
\(\Leftrightarrow x\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\end{cases}}\)
Vậy \(MinC=-36\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\end{cases}}\)

Tập hợp các điểm của đồ thị hàm số y = f(x) là
{(– 2; – 5); (– 1; – 2,5); (0; 0); (1; 2,5); (2; 5)}.
Biểu diễn các điểm trên trên cùng một mặt phẳng tọa độ ta được đồ thị hàm số y = f(x) như sau:

a) Có 22 ván người chơi gieo được tổng số chấm là 5 hoặc 7
Vậy xác suất thực nghiệm của biến cố E là \(\frac{{22}}{{80}} \approx 0,275\)
b) Có 7 ván người chơi gieo được tổng số chấm từ 10 trở lên
Vậy xác suất thực nghiệm của biến cố F là \(\frac{7}{{80}} \approx 0,0875\)

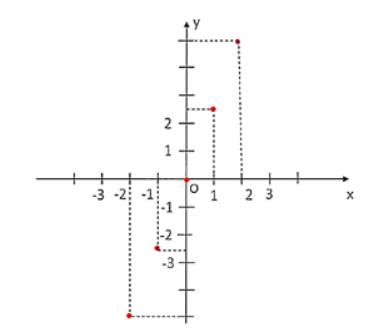
a có tập hợp các điểm của đồ thị hàm số y = f(x) là
{(– 3; 4); (– 1; 3,5); (1; 1); (2,5; 0)}.
Biểu diễn các điểm trên lên mặt phẳng tọa độ Oxy ta được đồ thị của hàm số y = f(x).
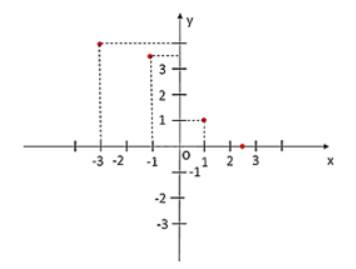

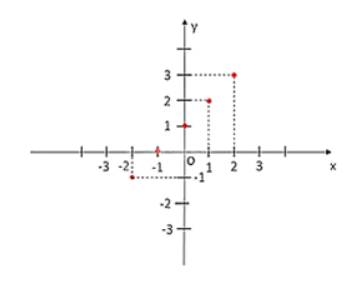
a) Tập hợp các cặp giá trị tương ứng của x và y là:
{(–2; –1); (–1; 0); (0; 1); (1; 2); (2; 3)}.
b) Ta biểu diễn các điểm đã cho như sau:

a) Có 7 học sinh có điểm 1, 9 học sinh có điểm 2, 11 học sinh có điểm 3, 11 học sinh có điểm 4, 12 học sinh có điểm 5 => Có 50 học sinh có điểm nhỏ hơn hoặc bằng 5
Xác suất thực nghiệm của biến cố A là: \(\frac{{50}}{{100}} = 0,5\)
Có 11 học sinh có điểm 4, 12 học sinh có điểm 5, 12 học sinh điểm 6, 13 học sinh điểm 7, 9 học sinh điểm 8, 8 học sinh điểm 9 => Có 65 học sinh có điểm từ 4 đến 9
Xác suất thực nghiệm của biến cố B là: \(\frac{{65}}{{100}} = 0,65\)
b) Gọi k là số học sinh có số điểm không vượt quá 5
Có \(P(A) \approx \frac{k}{{80}}\). Thay giá trị ước lượng của P(A) ở trên, ta được
\(\frac{k}{{80}} \approx 0,5\) => k ≈ 40
Vậy có khoảng 40 học sinh có số điểm không vượt quá 5
Gọi h là số học sinh có số điểm từ 4 đến 9 điểm
Có \(P\left( B \right) \approx \frac{h}{{80}}\). Thay giá trị ước lượng của P(B) ở trên, ta được
\(\frac{h}{{80}} \approx 0,65\)=> h≈52
Vậy có khoảng 52 học sinh có số điểm từ 4 đến 9 điểm