LT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
2
2 tháng 6 2016
Đặt x+y=a ta có:
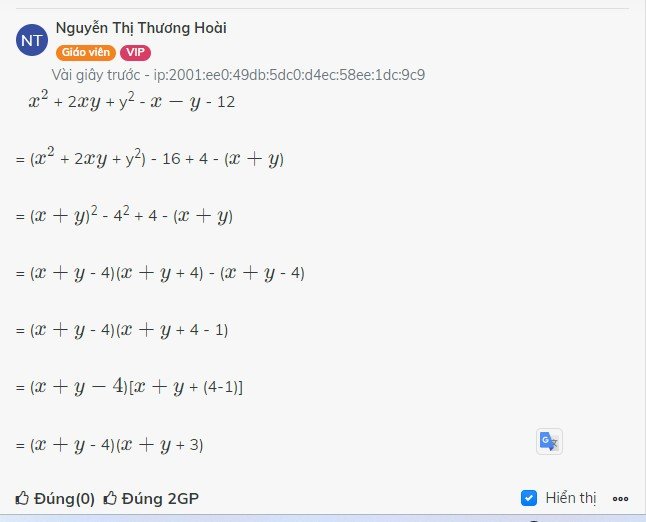
x2+2xy+y2-x-y-12=(x2+2xy+y2)-(x+y)-12=(x+y)2-(x+y)-12=a2-a-12=(a2+3a)-(4a+12)=a(a+3)-4(a+3)=(a+3)(a-4)=(x+y+3)(x+y-4).
NN
1
23 tháng 6 2016
a) \(x^2-x-y^2-y\)
\(=\left(x-y\right).1\)
b) \(x^2-2xy+y^2-z^2\)
\(=\left(x-y\right)^2-x^2\)
\(=\left(x-y-z\right)\left(x-y+z\right)\)
Mik tl nhanh nhất đấy
HN
1
LN
1
PL
15 tháng 7 2018
ax - ay + bx - by= (ax - ay) + (bx - by)
= a(x - y) + b(x - y)
= (x - y)(a + b)
x2 - 2xy + y2 - 1= (x2 - 2xy + y2) - 12
= (x - y)2 - 12
= (x - y - 1)(x - y + 1)
9 - x2 - 2xy - y2 = 32 - ( x2 + 2xy + y2 )
= 32 - ( x + y)2
= ( 3 - ( x + y)).(3 + ( x + y))
= (3 - x - y)(3 + x + y)
AX
3
KK
30 tháng 8 2015
bạn click vô đây Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
10 tháng 10 2021
ko phải phân tích đa thức thành nhân tử
là rút gọn biểu thức
hì hì
NB
1
DK
1
6 tháng 10 2016
a) \(x^2-x-y^2-y=\left(x^2-y^2\right)-\left(x+y\right)\\ =\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\)
b) \(x^2-2xy+y^2-z^2\)
\(=\left(x-y\right)^2-z^2=\left(x-y+z\right)\left(x-y-z\right)\)