
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2\left(x+y\right)-y\left(x^2-y^2\right)\)
\(=x^2\left(x+y\right)-y\left(x-y\right)\left(x+y\right)\)
\(=\left(x+y\right)\left[x^2-y\left(x-y\right)\right]\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3+y^3\)
Thay \(x=-6,y=8\) vào biểu thức đã rút gọn \(x^3+y^3\Rightarrow\left(-6\right)^3+8^3=296\)

a: =-3x^2y*x^2y+3x^2y*2xy
=-3x^4y^2+6x^3y^2
b: =x^3-x^2y+x^2y+y^2=x^3+y^2
c: =x*4x^3-x*5xy+2x*x
=4x^4-5x^2y+2x^2
d: =x^3+x^2y+2x^3+2xy
=3x^3+x^2y+2xy

\(g,\left(x^2y-xy+xy^2+y^3\right).3xy^2\\ =\left(3xy^2.x^2y\right)-\left(3xy^2.xy\right)+\left(3xy^2.xy^2\right)+\left(3xy^2.y^3\right)\\ =3x^3y^3-3x^2y^3+3x^2y^4+3xy^5\)
\(h,\dfrac{2}{3}x^2y\left(15x-0,9y+6\right)\\ =\left(\dfrac{2}{3}x^2y.15x\right)-\left(\dfrac{2}{3}x^2y.0,9y\right)+\left(\dfrac{2}{3}x^2y.6\right)\\ =10x^3y-\dfrac{3}{5}x^2y^2+4x^2y\)
\(i,-\dfrac{3}{7}x^4\left(2,1y^2-0,7x+35\right)\\ =\left(-\dfrac{3}{7}x^4.2,1y^2\right)-\left(-\dfrac{3}{7}x^4.0,7x\right)+\left(-\dfrac{3}{7}x^4.35\right)\\ =-\dfrac{9}{10}x^4y^2+\dfrac{3}{10}x^5-15x^4\)
g: =x^2y*3xy^2-xy*3xy^2+xy^2*3xy^2+y^3*3xy^2
=3x^3y^3-3x^2y^3+3x^2y^4+3xy^5
h: =2/3x^2y*15x-2/3x^2y*0,9y+2/3x^2y*6
=10x^3y-0,6x^2y^2+4x^2y
i: =-3/7x^4*2,1y^2+3/7x^4*0,7x-3/7x^4*35
=-0,9x^4y^2+3/10x^5-15x^4

a) \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x+2\right)\left(2-x\right)=1\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(x-2\right)=1\)
\(\Leftrightarrow\left(x^3-3^3\right)-x\left(x+2\right)\left(x-2\right)=1\)
\(\Leftrightarrow x^3-27-x\left(x^2-2^2\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
\(\Leftrightarrow4x-27=1\)
\(\Leftrightarrow4x=28\)
\(\Leftrightarrow x=7\)
b) \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow\left[\left(x+1\right)-\left(x-1\right)\right]\left[\left(x+1\right)^2+\left(x-1\right)\left(x+1\right)+\left(x-1\right)^2\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left[\left(x+1\right)^2+\left(x^2-1\right)+\left(x-1\right)^2\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left[\left(x^2+2x+1\right)+\left(x^2-1\right)+\left(x^2-2x+1\right)\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left(x^2+2x+1+x^2-1+x^2-2x+1\right)-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left(3x^2+1\right)-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow6x^2+2-6\left(x^2-2x+1\right)=-10\)
\(\Leftrightarrow6x^2+2-6x^2+12x-6=-10\)
\(\Leftrightarrow12x-4=-10\)
\(\Leftrightarrow12x=-6\)
\(\Leftrightarrow x=-\dfrac{6}{12}=-\dfrac{1}{2}\)
\(a,\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\\ \Leftrightarrow x^3-3x^2+3x^2-9x+9x-27+\left(x^2+2x\right)\left(2-x\right)-1=0\\ \Leftrightarrow x^3-3x^2+3x^2-9x+9x-27+2x^2-x^3+4x-2x^2-1=0\\ \Leftrightarrow x^3-x^3-3x^2+3x^2+2x^2-2x^2-9x+9x+4x=1+27\\ \Leftrightarrow4x=28\\ \Leftrightarrow x=7\)

b: 4x^2+4x+1=(2x+1)^2
c: =(6x+1)^2
d: =(3x-4y)^2
e: =(1/2x+2y)^2
f: =-(x^2-10x+25)
=-(x-5)^2
g: =-(16a^4b^6+24a^5b^5+9a^6b^4)
=-a^4b^4(16b^2+24ab+9a^2)
=-a^4b^2(4b+3a)^2
h: =(5x)^2-2*5x*2y+(2y)^2
=(5x-2y)^2
i: =(5x^2)^2-2*5x^2*y+y^2
=(5x^2-y)^2

d) \(\left(3x+1\right)^2-4\left(x-2\right)^2\)
\(=\left[\left(3x+1\right)-2\left(x-2\right)\right]\left[\left(3x+1\right)+2\left(x-2\right)\right]\)
\(=\left(3x+1-2x+4\right)\left(3x+1+2x-4\right)\)
\(=\left(x+5\right)\left(5x-3\right)\)
c) \(9\left(2x+3\right)^2-4\left(x+1\right)^2\)
\(=\left[3\left(2x+3\right)-2\left(x+1\right)\right]\left[3\left(2x+3\right)+2\left(x+1\right)\right]\)
\(=\left(6x+9-2x-2\right)\left(6x+9+2x+2\right)\)
\(=\left(4x-7\right)\left(8x+11\right)\)
f) \(4b^2c^2-\left(b^2+c^2-a^2\right)^2\)
\(=\left[2bc-\left(b^2+c^2-a^2\right)\right]\left[2bc+\left(b^2+c^2-a^2\right)\right]\)
\(=\left(2bc-b^2-c^2+a^2\right)\left(2bc+b^2+c^2-a^2\right)\)
g: =(ax+by-ay-bx)(ax+by+ay+bx)
=[a(x-y)-b(x-y)]*[a(x+y)+b(x+y)]
=(x-y)(x+y)(a-b)(a+b)
h: =(a^2+b^2-5-2ab-4)(a^2+b^2-5+2ab+4)
=[(a-b)^2-9][(a+b)^2-1]
=(a-b-3)(a-b+3)(a+b-1)(a+b+1)
i: =(4x^2-3x-18-4x^2-3x)(4x^2-3x-18+4x^2+3x)
=(-6x-18)(8x^2-18)
=-12(x+3)(4x^2-9)
=-12(x+3)(2x-3)(2x+3)
k: =(3x+3y-3)^2-(4x+6y+2)^2
=(3x+3y-3-4x-6y-2)(3x+3y-3+4x+6y+2)
=(-x-3y-5)(7x+9y-1)
i: =25-(2x-3y)^2
=(5-2x+3y)(5+2x-3y)
m: =(x-y)^2-(2m-n)^2
=(x-y-2m+n)(x-y+2m-n)

\(a,3\left(2a-1\right)+5\left(3-a\right)\)
\(=6a-3+15-5a\)
\(=a-12\)
Thay \(a=\dfrac{-3}{2}\) vào biểu thức trên
\(a-12\)
\(=\dfrac{-3}{2}-12\)
\(=\dfrac{-27}{2}\)
\(b,25x-4\left(3x-1\right)+7\left(5-2x\right)\)
\(=25x-12x+4+35-14x\)
\(=-1x+39\)
Thay \(x=2,1\) vào biểu thức trên
\(-1x+39\)
\(=-1.2,1+39\)
\(=-2,1+39\)
\(=36,9\)
\(c,4a-2\left(10a-1\right)+8a-2\)
\(=4a-20a+2+8a-2\)
\(=-8a\)
Thay \(a=-0,2\) vào biểu thức trên
\(-8a\)
\(=-8.\left(-0,2\right)\)
\(=1,6\)
\(d,12\left(2-3b\right)+35b-9\left(b+1\right)\)
\(=24-36b+35b-9b-9\)
\(=-10b-15\)
Thay \(b=\dfrac{1}{2}\) vào biểu thức trên
\(-10b-15\)
\(=-10.\dfrac{1}{2}-15\)
\(=-20\)

a: =6y^3-3y^2-y^2+2y-y+y^2-y^3
=5y^3-3y^2+y
b: =2x^2a-a-2x^2a-a-x^2-ax
=-x^2-ax-2a
c: =2p^3-p^3+1+2p^3+6p^2-3p^5
=3p^3+6p^2-3p^5+1
d: =-3a^3+5a^2+4a^3-4a^2=a^3+a^2
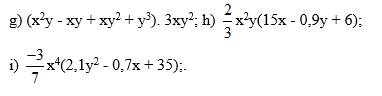
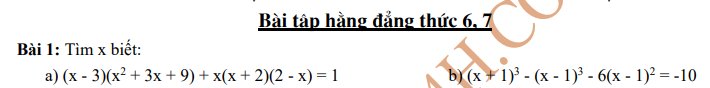
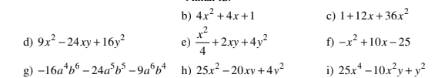




x+1276=1785+2576
<=>x+1276=4361
<=>x=4361-1276
<=>x=2985
Vậy tập nghiệm của phương trình là S={2985}
\(x+1276=1785+2576\)
\(\Leftrightarrow x=1785+2576-1276\)
\(\Leftrightarrow x=2985\)
Tập nghiệm: \(S=\left\{2985\right\}\)