Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

n( 3n - 2 ) - 3n( n + 2 )
= 3n2 - 2n - 3n2 - 6n
= -8n luôn chia hết cho ±1 ; ±2 ; ±4 ; ±8

n(4n-1)-4n(n+2)=4n2-n-4n2-8n=-9n
=>n(4n-1)-4n(n+2) luôn chia hết cho 9

Ta có: \(n^5-5n^3+4n=n\left(n^4-5n^2+4\right)\) \(=n\left(n^4-n^2-4n^2+4\right)\) \(=n\left[n^2\left(n^2-1\right)-4\left(n^2-1\right)\right]\) \(=n\left(n^2-1\right)\left(n^2-4\right)\) \(=n\left(n-1\right)\left(n+1\right)\left(n-2\right)\left(n+2\right)\) \(=\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\) Vì \(\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)\) là tích của 5 số tự nhiên liên tiếp nên chia hết cho 3 ; 5 và 8. Mà 3.5.8 = 120. => \(n^5-5n^3+4n⋮120\) Vậy ...
A = n^5 - 5n^3 + 4n = n.(n^4 - 5n^2+4)
= n.( n^4 - 4n^2 - n^2 + 4)
= n.[ n^2.(n^2 - 1) - 4.(n^2 - 1)
= n.(n^2) . (n^2 - 4)
= n.(n-1).(n+1).(n+2).(n-2)
A chia hết cho 120 (vìđây là 5 số liên tiếp, vì thế nó chia hết cho 2, 3, 4, 5.
Mà 2.3.4.5=120 nên A chia hết cho 120 Với mọi n thuộc Z.)

\(n\left(5n-1\right)-5n\left(n+2\right)=5n^2-n-5n^2-10n=-11n⋮11\forall n\in Z\)

\(A=\left(2n^2\right)^2+2.\left(2n^2\right).\left(3n\right)+\left(3n\right)^2-4n^2-6n+1\)
\(=\left(2n^2+3n\right)^2-2.\left(2n^2+3n\right)+1=\left(2n^2+3n-1\right)^2\)

\(4n^2\left(n+2\right)+4n\left(n+2\right)=\left(n+2\right)\left(4n^2+4n\right)=4n\left(n+1\right)\left(n+2\right)\)
Đặt \(A=n\left(n+1\right)\left(n+2\right)\) ta có
+ Nếu n chẵn => A chia hết cho 2
+ Nếu n lẻ thì n+1 chia hết cho 2 => A chia hết cho 2
=> A chia hết cho 2 với mọi n
+ Nếu n chia hết cho 3 => A chia hết cho 3
+ Nếu n chia 3 dư 1 thì n+2 chia hết cho 3 => A chia hết cho 3
+ Nếu n chia 3 dư 2 thì n+1 chia hết cho 3 => A chia hết cho 3
=> A chia hết cho 3 với mọi n
=> A đồng thời chia hết cho cả 2 và 3 với mọi n => A chia hết cho 6 với mọi n => A có thể biểu diễn thành A=6.k
=> 4A=4.6.k=24.k chia hết cho 24 (dpcm)
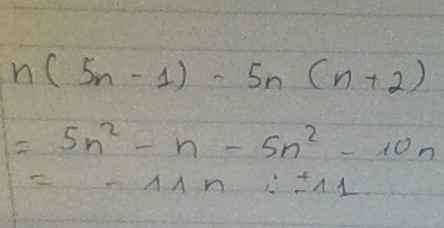
Ta có:
\(n\left(5n-2\right)-5n\left(n+3\right)\)
\(=n\left(5n-2\right)-n\left(5n+3\right)\)|
\(=n\left(5n-2-5n-3\right)=-5n\) ; Vì \(n\in Z\)
\(\Rightarrow-5n\in Z\Rightarrow -5n⋮-5\)
Vậy: .......
#HọcTốt!!