Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
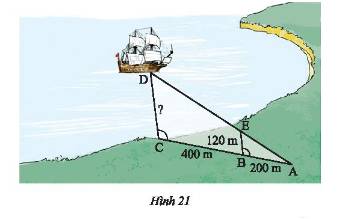
Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).
Ta có: \(AC = AB + BC = 200 + 400 = 600m\)
Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).
Vậy \(CD = 360m\).
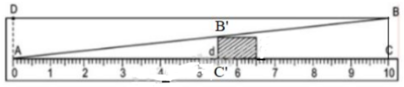
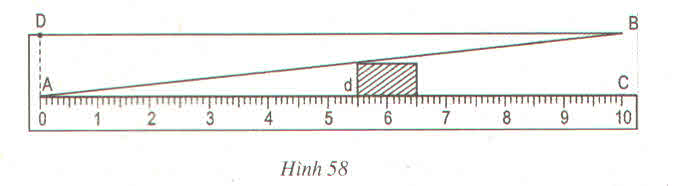
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC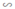 
ΔAB’C’ (vì B’C’ // BC).
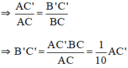
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.
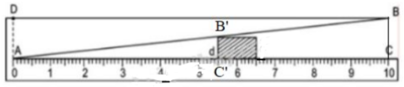
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC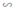 
ΔAB’C’ (vì B’C’ // BC).
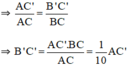
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.
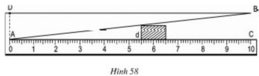
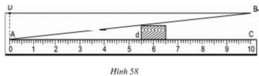
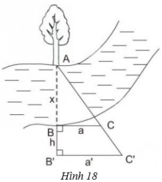
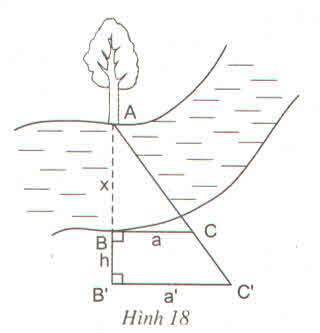
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 
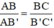(hệ quả định lý Talet)
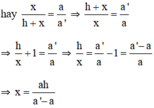
Ta có:
ABAB′ABAB′ = BCBC′BCBC′ mà AB' = x + h nên
xx+hxx+h = aa′aa′ <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x= aha′−aaha′−a
Vậy khoảng cách AB bằng aha′−a
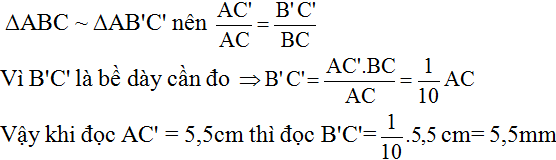
![[IMG]](https://diendan.hocmai.vn/file:///C:/Users/NDC/AppData/Local/Temp/msohtml1/01/clip_image002.gif)
Vì \(\widehat {ABE} = \widehat {ACD} \Rightarrow BE//CD\) (hai góc đồng vị bằng nhau)
Trong tam giác \(ACD\) có \(BE//CD\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}}\) mà \(AC = AB + BC = 8 + 8 = 16\)
Suy ra, \(\frac{8}{{16}} = \frac{3}{{CD}} \Rightarrow CD = \frac{{3.16}}{8} = 6\).
Vậy bề rộng \(CD\) của con sông là 6m.