Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Với một cái thước dây liệu có thể xác định được thể tích của một vật thể có dạng hình cầu hay không?

Dùng thước dây tạo ra đường tròn đặt vừa khía hình cầu .Khi đó độ dài của đường tròn là C .Suy ra : 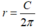
Thể tích của vật thể : 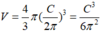

Diện tích sân hình vuông là:
3,5 x 3,5 = 12,25 ( m2 )
Diện tích viên gạch là:
25 x 100 = 2500 ( cm2 ) = 25 m2
Không thể lát gạch có kích thước 25 cm x 100 cm mà ko cắt vì kích thước gạch lớn hơn diện tích sân
Diện tích một viên gạch hình chữ nhật là: \(25\cdot100=2500\left(cm^2\right)=0,25m^2\)
Diện tích cái sân là: \(3,5\cdot3,5=12,25\left(m^2\right)\)
Vậy số viên gạch cần để lát cái sân đó là: \(12,25:0,25=49\)(viên gạch)
Vì 12,25 chia hết cho 0,25 nên không cần cắt gạch mà vẫn lát được hết cái sân

a) Hình cầu bán kính r, vậy thể tích của nó là 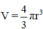
b) Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: V 1 = π r 2 ⋅ 2 r = 2 π r 3
c) Thể tích hình trụ trừ đi thể tích hình cầu là:
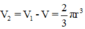
d) Thể tích hình nón có bán kính đáy r, chiều cao 2r
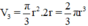
e) Từ các kết quả trên suy ra: Thể tích hình nón "nội tiếp" trong một hình trụ thì bằng thể tích hình trụ trừ đi thể tích hình cầu nội tiếp trong hình trụ ấy.
Hoặc: Thể tích hình trụ bằng tổng thể tích hình nón và hình cầu nội tiếp hình trụ.

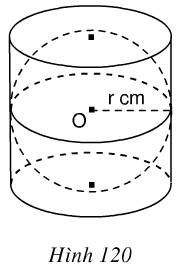
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính:
a)Thể tích hình cầu.
b) Thể tích hình trụ.
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm.
e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
Hướng dẫn trả lời:
a) Thể tích của hình cầu là:
V1=43πr3(cm3)V1=43πr3(cm3)
b) Thể tích hình trụ là:
V2 = πr2. 2r = 2πr3 (cm3)
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu là:
V3=V2−V1=2πr3−43πr2=23πr3(cm3)V3=V2−V1=2πr3−43πr2=23πr3(cm3)
d) Thể tích hình nón là:
V4=π3r2.2r=23πr3(cm3)V4=π3r2.2r=23πr3(cm3)
e) Từ kết quả ở câu s, b,c, d ta có hệ thức: V4 = V2 – V1 hay “ Thể tích hình nón nội tiếp trong hình trụ bằng hiệu giữa thể tích hình trụ và thể tích hình cầu nội tiếp trong hình trụ ấy”

Hướng dẫn trả lời:
a) Thể tích của hình cầu là:
V1=43πr3(cm3)V1=43πr3(cm3)
b) Thể tích hình trụ là:
V2 = πr2. 2r = 2πr3 (cm3)
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu là:
V3=V2−V1=2πr3−43πr2=23πr3(cm3)V3=V2−V1=2πr3−43πr2=23πr3(cm3)
d) Thể tích hình nón là:
V4=π3r2.2r=23πr3(cm3)V4=π3r2.2r=23πr3(cm3)
e) Từ kết quả ở câu s, b,c, d ta có hệ thức: V4 = V2 – V1 hay “ Thể tích hình nón nội tiếp trong hình trụ bằng hiệu giữa thể tích hình trụ và thể tích hình cầu nội tiếp trong hình trụ ấy”

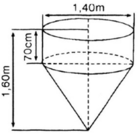
a) Thể tích cần tính gồm một hình trụ, đường kính đáy 1,4m, chiều cao 70cm = 0,7m, và một hình nón, bán kính đáy bằng bán kính đáy của hình trụ, chiều cao hình nón 0,9m.


-0133-1.jpg)
Dùng thước dây tạo ra đường tròn đặt vừa khít hình cầu, như vậy biết được độ dài đường tròn lớn là l từ đó thể tích hình cầu sẽ là \(\dfrac{l^3}{6\pi^2}\)