Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Đáp án C
Ta có: y’ = 3x2 + 2(m+1)x – (3m+2)
Hàm số đồng biến trên khoảng (0;1)
3x2 + 2(m+1)x – (3m+2) ≥ 0 ∀ x ∈ (0;1)
⇔ m ≤ − 3 x 2 + 2 x − 2 2 x − 3 ∀ x ∈ (0;1)
Xét hàm số: g = − 3 x 2 + 2 x − 2 2 x − 3 D =(0;1)
Ta có: g’ = − 6 x 2 − 18 x − 2 ( 2 x − 3 ) 2
ð g’ = 0 ⇔ x = 9 ± 93 6 (không thoản mãn)
Ta có bảng biến thiên
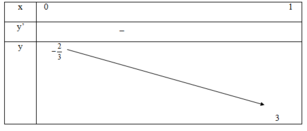
Vậy với m ≤ 3 hàm số đồng biến trên khoảng (0;1)
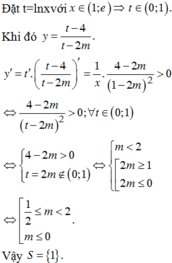
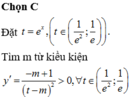
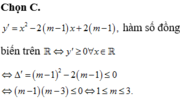
Đáp án C
Đặt t = e x do x ∈ - 2 ; - 1 ⇒ t ∈ 1 e 2 ; 1 e khi đó y = t - 1 t - m t ≠ m
Ta có y ' = - m + 1 t - m 2 , để hàm số đồng biến - m + 1 > 0 m ∈ 1 e 2 ; 1 e ⇒ [ m ≤ 1 e 2 1 e ≤ m < 1