Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: A
Giả sử d cắt hai trục tọa độ tại M(a;0), N(0;b)
Vì tam giác OMN cân tại O nên |a| = |b|
Vì d đi qua A(1;-2) nằm ở góc phần tư thứ tư nên b = -a, a > 0
Suy ra, phương trình d có dạng:
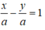
Vì A(1;-2) thuộc d nên:
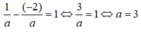
Vậy phương trình d là:
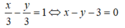

Đề bài không chính xác, chỉ có thể tìm d để biểu thức đạt GTNN chứ ko tồn tại đường thẳng để biểu thức đạt GTLN

Giả sử A là giao của d với Ox và B là giao của d với Oy
\(\Rightarrow A\left(a;0\right)\) và \(B\left(0;b\right)\)
Do I là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{a+0}{2}\\y_I=\dfrac{b+0}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=4\\b=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}A\left(4;0\right)\\B\left(0;-2\right)\end{matrix}\right.\)
Phương trình d theo đoạn chắn:
\(\dfrac{x}{4}+\dfrac{y}{-2}=1\Leftrightarrow x-2y-4=0\)

Đáp án: D
Đường thẳng d đi qua A cắt Ox, Oy tại hai điểm M, N có dạng:
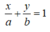
Vì tam giác OMN cân nên |a| = |b|
Vì d đi qua A(2;-1) nằm ở góc phần tư thứ tư nên b = -a, a > 0
Suy ra, đường thẳng MN có dạng:
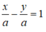
MN đi qua A(2;-1) nên
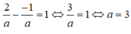
Vậy đường thẳng MN có dạng:
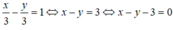

Đường thẳng d đi qua 2 điểm M(a;0) \(\left(a\ne0\right)\) và N(0;b)(\(\left(b\ne0\right)\) có phương trình :
\(\frac{x}{a}+\frac{y}{b}=1\)
Đường thẳng d đi qua A(2;-1):
\(\frac{2}{a}+\frac{-1}{b}=1\)
\(\Leftrightarrow2b-a=ab\left(@\right)\)
\(\overrightarrow{OM}=\left(a;0\right);\overrightarrow{ON}=\left(0;b\right)\)
\(OM=\sqrt{a^2}\)
\(ON=\sqrt{b^2}\)
\(OM=2ON\Leftrightarrow OM^2=4ON^2\)
\(\Leftrightarrow a^2=4b^2\Leftrightarrow\left[{}\begin{matrix}a=2b\\a=-2b\end{matrix}\right.\)
Thay a=2b vào (@) được b=0 (loại)
Thay a=-2b vào (@) được \(\left[{}\begin{matrix}b=0\left(lọai\right)\\b=-2\left(nhan\right)\end{matrix}\right.\)
\(b=-2\Rightarrow a=4\)
Vậy phương trình d :\(\frac{x}{4}-\frac{y}{2}=1\)