Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: y=ax+b
a=tan alpha=1
=>y=x+b
Thay x=-1 và y=1 vào (d), ta được:
b-1=1
=>b=2
=>y=x+2
d: (Δ)//(d) nên Δ: 3x+4y+c=0
(C): x^2+y^2-2x+2y-7=0
=>x^2-2x+1+y^2+2y+1=9
=>(x-1)^2+(y+1)^2=9
=>R=3; I(1;-1)
Theo đề, ta có: d(I;Δ)=3
=>\(\dfrac{\left|1\cdot3+\left(-1\right)\cdot4+c\right|}{\sqrt{3^2+4^2}}=3\)
=>|c-1|=3*5=15
=>c=16 hoặc c=-14

Chọn D.
Ta có: ± b a = ± 2 3 ⇒ a = 3 b = 2 .
Phương trình (H) : x 2 9 - y 2 4 = 1

Đáp án: D
Hypebol có hai đường tiệm cận
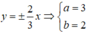
Vậy phương trình của hypebol là:
x 2 9 - y 2 4 = 1

F1(\(-\sqrt{3};0\)) => c=\(\sqrt{3}\)
có: \(b^2=a^2-c^2=a^2-3\)
pt elip di qua M:
\(\dfrac{3}{a^2}+\dfrac{1}{4b^2}=1\)
\(\Leftrightarrow\dfrac{3}{a^2}+\dfrac{1}{4a^2-12}=1\)
dat a^2=t (t>0)
\(\Leftrightarrow\dfrac{3}{t}+\dfrac{1}{4t-12}=1\\ \Leftrightarrow12t-36+t=4t^2-12t\)
\(\Leftrightarrow4t^2-25t+36=0\\ \Leftrightarrow\left[{}\begin{matrix}t=4\\t=\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a^2=4\\a^2=\dfrac{9}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}b^2=1\\b^2=-\dfrac{3}{4}\left(loai\right)\end{matrix}\right.\)
=>ptelip: \(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1\)
