Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\orbr{\begin{cases}x-\frac{13}{18}y=0\\x-\frac{18}{13}y=0\end{cases}}\)
Đáp án A
Phương án D không phải là hệ phương trình bậc nhất hai ẩn nên loại D
Hệ phương trình có chứa phương trình bậc hai là hệ phương trình ở đáp án D nên loại D
+ Với hệ phương trình A:
x − y = − 2 x + y = 4 ⇒ 1 − 3 = − 2 1 + 3 − 4 ⇔ − 2 = − 2 4 = 4 (luôn đúng) nên (1; 3) là nghiệm của hệ phương trình x − y = − 2 x + y = 4
+ Với hệ phương trình B: 2 x − y = 0 x + y = 4
Thay x = 1; y = 3 ta được 2.1 − 3 = 0 1 + 3 = 4 ⇔ − 1 = 0 1 + 3 = 4 (vô lý) nên loại B.
+ Với hệ phương trình C: x + y = 4 2 x + y = 4
Thay x = 1; y = 3 ta được 1 + 3 = 4 2.1 + 3 = 4 ⇔ 4 = 4 5 = 4 (vô lý) nên loại C.
Đáp án:A
\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ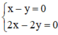 
và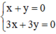 
Hệ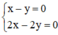 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ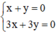 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
Theo đề, ta có: ax+by=c
\(\Leftrightarrow\left\{{}\begin{matrix}2a=c\\a+2b=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{c}{2}\\b=\dfrac{1}{4}c\end{matrix}\right.\)
b=1/4c thì 1/4 ở đâu z