Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
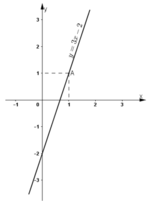
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
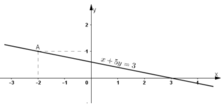
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 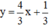
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
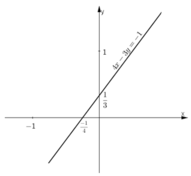
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 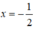
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
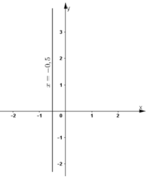
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
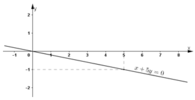
f) 0x + 2y = 5
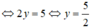
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
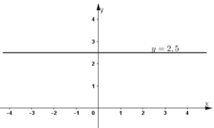
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.


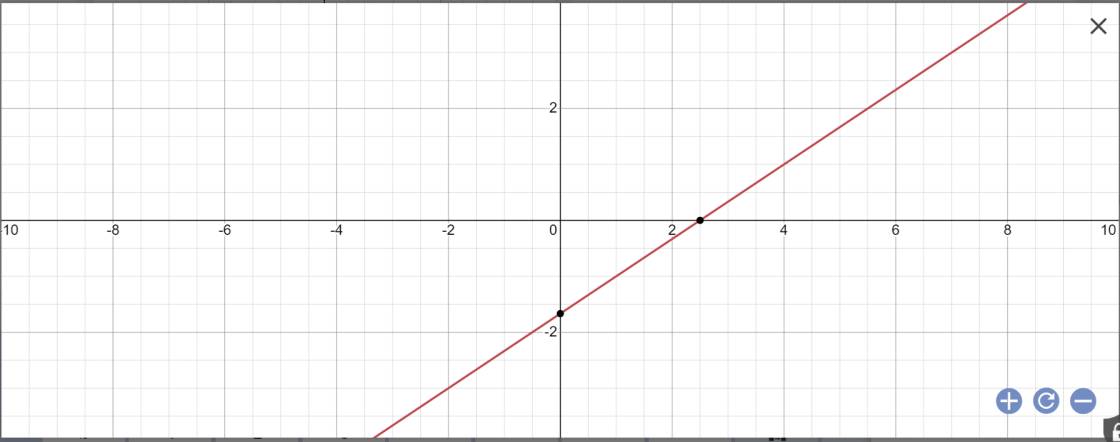
a: 2x-3y=5
=>3y=2x-5
=>\(y=\dfrac{2}{3}x-\dfrac{5}{3}\)
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x-\dfrac{5}{3}\end{matrix}\right.\)
Biểu diễn tập nghiệm:
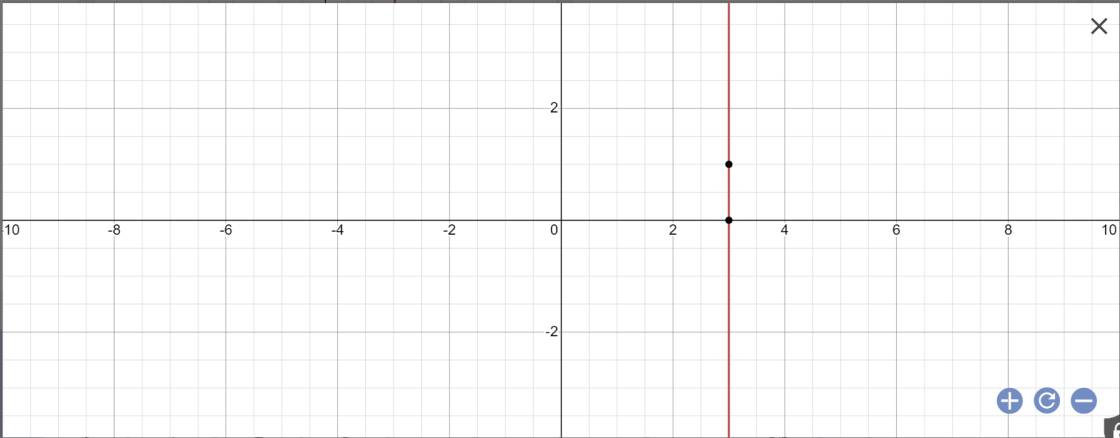
b: 4x+0y=12
=>4x=12
=>x=3
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x=3\\y\in R\end{matrix}\right.\)
Biểu diễn tập nghiệm:
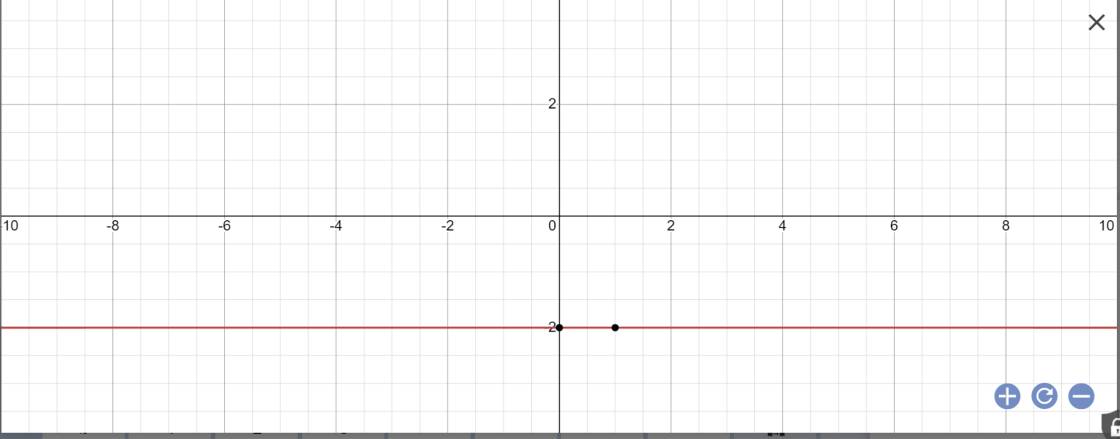
c: 0x-3y=6
=>-3y=6
=>y=-2
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=-2\end{matrix}\right.\)
Biểu diễn tập nghiệm:

a: 2x-y=3
nên y=2x-3
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=2x-3\end{matrix}\right.\)
b: x+2y=4
nên x=4-2y
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=4-2y\end{matrix}\right.\)
c: 3x-2y=6
nên 3x=2y+6
hay \(x=\dfrac{1}{2}y+2\)
Vậy: Nghiệm là \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{1}{2}y+2\end{matrix}\right.\)
d: 2x+3y=5
nên 2x=5-3y
hay x=-3/2y+5/2
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=-\dfrac{3}{2}y+\dfrac{5}{2}\end{matrix}\right.\)

a: Thay x=-1 và y=2 vào (1), ta được:
\(\left(2m-1\right)\cdot\left(-1\right)+\left(2m-2\right)\cdot2=4\)
=>-2m+1+4m-4=4
=>2m-3=4
=>m=7/2
=>(1): 6x+5y=4
=>x=(4-5y)/6
=>Nghiệm tổng quát là:
\(\left\{{}\begin{matrix}y\in R\\x=\dfrac{4-5y}{6}\end{matrix}\right.\)
b:
(1): (2m-1)x+(2m-2)y=4
Ox: y=0
=>0x+y+0=0
Để (1)//Ox thì 2m-1=0 và 2m-2=1
=>\(m\in\varnothing\)
Oy: x=0
=>x+0y+0=0
Để (1)//Oy thì 2m-1=1 và 2m-2=0
=>m=1

a: Thay x=-1 và y=2 vào (1), ta được:
\(\left(2m-1\right)\cdot\left(-1\right)+\left(2m-2\right)\cdot2=4\)
=>-2m+1+4m-4=4
=>2m-3=4
=>m=7/2
=>(1): 6x+5y=4
=>x=(4-5y)/6
=>Nghiệm tổng quát là:
\(\left\{{}\begin{matrix}y\in R\\x=\dfrac{4-5y}{6}\end{matrix}\right.\)
b:
(1): (2m-1)x+(2m-2)y=4
Ox: y=0
=>0x+y+0=0
Để (1)//Ox thì 2m-1=0 và 2m-2=1
=>\(m\in\varnothing\)
Oy: x=0
=>x+0y+0=0
Để (1)//Oy thì 2m-1=1 và 2m-2=0
=>m=1

Bài 1:
Thay, thử giá trị $(x,y)=(-2,3)$ vào các phương trình trong các đáp án, ta thấy chỉ phương trình $b$ thỏa mãn : $2.(-2)+3.3=5$ nên cặp số đã cho là nghiệm của PT (b)
Bài 2:
Để $(-2;1)$ là nghiệm của pt đã cho thì khi thay giá trị $x=-2;y=1$ vào pt thì phải thỏa mãn.
\(m.2-5.(-1)=3m-1\)
\(\Rightarrow 2m+5=3m-1\Rightarrow m=6\)
Bài 3:
Đặt pt bậc nhất 2 ẩn là $ax+y=c$
Vì PT trên có nghiệm \((0;-2); (2;-5)\) nên:
\(\left\{\begin{matrix} a.0+(-2)=c\\ a.2+(-5)=c\end{matrix}\right.\Rightarrow \left\{\begin{matrix} -2=c\\ 2a=c+5\end{matrix}\right.\) \(\Rightarrow \left\{\begin{matrix} c=-2\\ 2a=-2+5=3\rightarrow a=\frac{3}{2}\end{matrix}\right.\)
Do đó \(\frac{3}{2}x+y=-2\) \(\Leftrightarrow 3x+2y=-4\)
Vậy PT bậc nhất 2 ẩn có dạng $3x+2y=-4$
Câu 6:
Thay lần lượt các cặp số đã cho vào PT $3x-2y=13$ ta thấy cặp $(-1,-8); (3,-2)$ là 2 cặp thỏa mãn nên đây là 2 cặp nghiệm của phương trình.

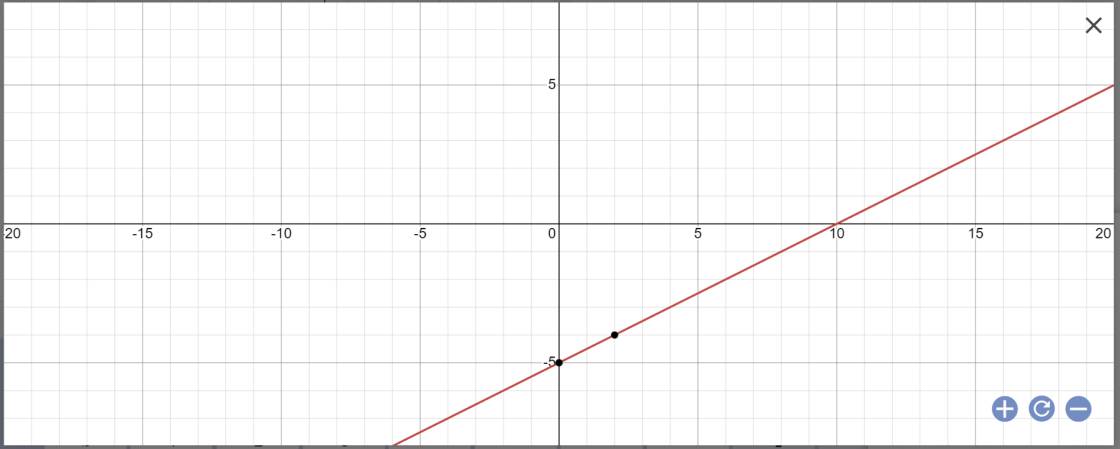
a: x-2y=5
=>2y=x-5
=>y=1/2x-5
Nghiệm tổng quát là: \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{1}{2}x-5\end{matrix}\right.\)
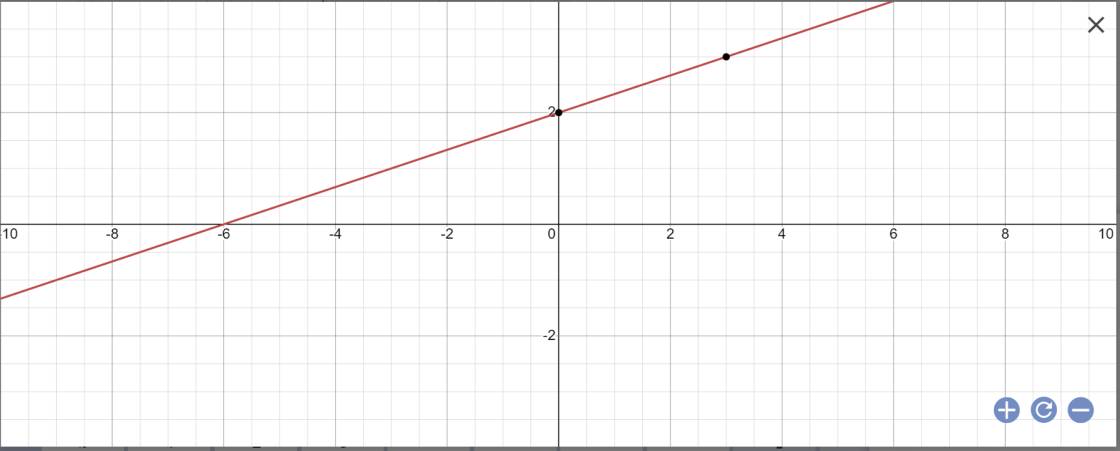
b: 3y-x=2
=>3y=x+2
=>y=1/3x+2
Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{1}{3}x+2\end{matrix}\right.\)
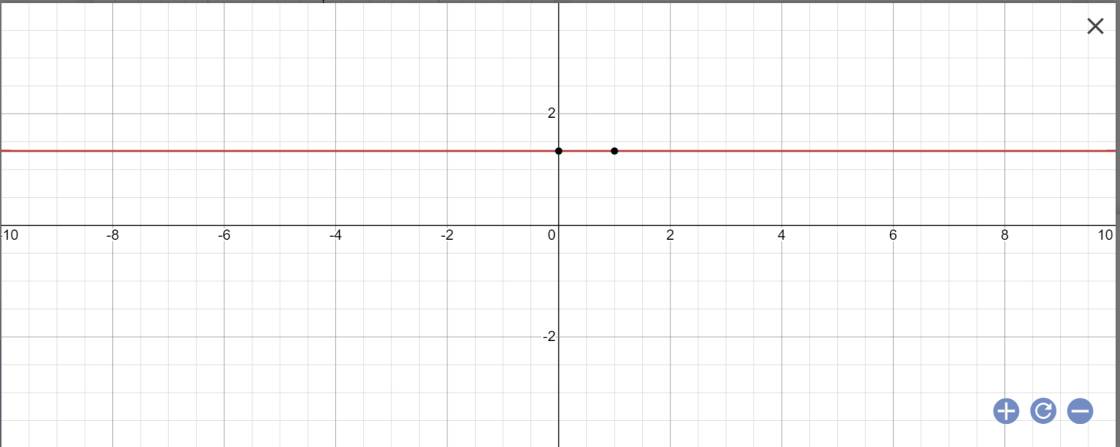
c: 0x+3y=4
=>3y=4
=>y=4/3
=>Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{4}{3}\end{matrix}\right.\)
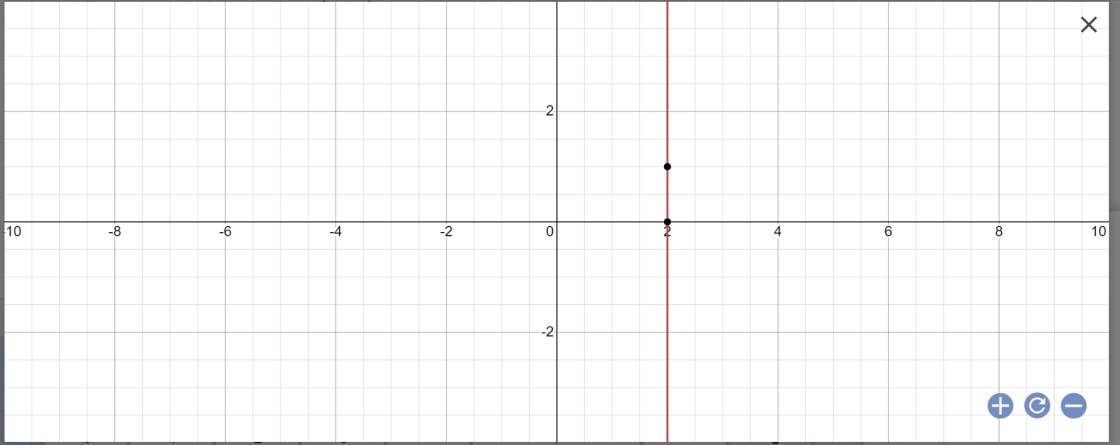
d: 2x+0y=4
=>2x=4
=>x=2
=>Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=2\\y\in R\end{matrix}\right.\)
a: 2x-3y=5
=>2x=3y+5
=>\(x=\dfrac{3}{2}y+\dfrac{5}{2}\)
vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{3}{2}y+\dfrac{5}{2}\end{matrix}\right.\)
Biểu diễn:
b: 0x+y=3
=>y=3
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=3\end{matrix}\right.\)
Biểu diễn:
c: x+0y=-2
=>x=-2
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=-2\\y\in R\end{matrix}\right.\)
Biểu diễn: