K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 10 2016
1
a) vẽ c ⊥ a.
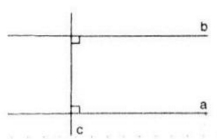
b) Vẽ như hình trên.
a song song với b do a và b đều vuông góc với c (Từ vuông góc đến song song)
2 a .Hình vẽ tương tự như câu 1.
B. b và c vuông góc với nhau do b // a mà a ⊥ c. (tính chất từ vuông góc đến song song)
3 a. câu này bn tự vẽ nhé
B. Giả sử b không song song với c thì b cắt c tại một điểm O nào đó. khi đó qua O ta có thể vẽ được hai đường thẳng b và c cùng song song với a. Điều đó trái với tiên để Ơclit về đường thẳng song song. Vậy b// c.
Tíck cho mk nha !
11 tháng 10 2016
1 )
a , b )
Vì c \(\perp\) a ( 1 )
c \(\perp\) b ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\) a // b
Ta có hình vẽ :
a b c
8 tháng 8 2018
a) a b c
Ta có :
a//b
a vuông góc với c => b vuông góc với c ( theo chuyên đề )
b) Ủa góc A vs góc B đâu vậy bạn ?
NN
8 tháng 8 2018
a) co vi a//b va \(a\perp c\)nen \(a\perp b\)
b) goc A nam o dau ?....
20 tháng 10 2016
a^2=cb
=> aa=cb
=>a/c=b/a=a+b/c+a=a-b/c-a
=>a+b/a-b=c+a/c-a
Q
20 tháng 4 2017
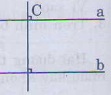
a) Vẽ c ⊥ a.
b) Vẽ b ⊥ c. Ta được a song song với b vì c cắt a và b trong các góc tạo thành có một cặp góc so le trong bằng nhau bằng 900.
c) Phát biểu tình chất bằng lời: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
5 tháng 11 2017
\(a\frac{1}{b}:b\frac{1}{a}=\frac{ab+1}{b}:\frac{ab+1}{a}=\frac{ab+1}{b}\cdot\frac{a}{ab+1}=\frac{a}{b}\)
11 tháng 9 2018
\(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\Rightarrow\frac{b-a}{ab}=\frac{1}{a-b}\Rightarrow\left(a-b\right)\left(b-a\right)=ab\Rightarrow-\left(a-b\right)^2=ab\)
mà \(-\left(a-b\right)^2\le0\forall\left\{a;b\right\}\Rightarrow ab\le0\forall\left\{a;b\right\}\)=> a và b ko thể cùng dương
Vậy, ko tồn tại 2 số nguyên dương a và b
11 tháng 9 2018
Ta có: 1/a -1/b = 1/(a-b) => (b-a)/ab = 1/(a-b) => (a-b)(a-b)= -ab (vô lí do (a-b)^2 lớn hơn hoặc =0 và ab dương)
=> Không tồn tại.
DL
27 tháng 7 2017
\(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
\(\Leftrightarrow\frac{b-a}{ab}=\frac{1}{a-b}\)
\(\Leftrightarrow\frac{\left(b-a\right)\left(b-a\right)}{ab\left(a-b\right)}=\frac{ab}{\left(a-b\right)ab}\)
\(\Leftrightarrow-\left(b-a\right)^2=ab\)
Áp dụng BĐT cô-si ta có : \(a^2+b^2\ge4ab\)
Vậy không có a,b thỏa mãn
24 tháng 5 2016
\(a\frac{1}{b}=a+\frac{1}{b}=\frac{ab+1}{b}\)
\(b\frac{1}{a}=b+\frac{1}{a}=\frac{ab+1}{a}\)
=> \(\frac{a\frac{1}{b}}{b\frac{1}{a}}=\frac{ab+1}{b}:\frac{ab+1}{a}=\frac{ab+1}{b}.\frac{a}{ab+1}=\frac{a}{b}\)
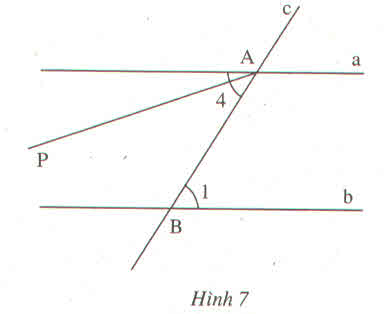
A B a b
Ta có \(\widehat{A}=\widehat{B}=90^o\)
Mà 2 góc này là 2 góc trong cùng phía bù nhau
=> a//b
Trong cùng phía bù nhau??