K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

KM
16 tháng 4 2019
A B C D
Chu vi tam giác ABC là:
6+3+4=13(cm)
Chu vi tam giác ADB là:
6+3+4=13(cm)
ĐS: Chu vi tam giác ABC và tam giác ADB= 13 cm
K CHO MIK NHA

YN
30 tháng 4 2021
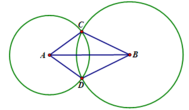
Vì C và D thuộc đường tròn ( A; 3cm ) nên ta có:
AC = AD = 3cm ( bằng bán kính đường tròn tâm A )
Vì C và D thuộc đường tròn ( B; 4cm ) nên ta có:
BC = BD = 4cm ( bằng bán kính đường tròn tâm B )
Chu vi tam giác ACB là:
AB + AC + BC = 3 + 6 + 4 = 13 cm
Chu vi tam giác ADB là: C D B A
AD + DB + AB = 3 + 4 + 6 = 13 cm

8 tháng 5 2020
chu vi tam giac ABC la :
6 + 3 + 4 = 13 cm
chu vi tam giac ADB la :
6 + 3 + 4 = 13 cm
hok tot