Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ đường cao AH của ∆PQR
=> H là trung điểm của QR
=> HR = 1/2QR = 3cm
+ ∆PHR vuông tại H
nên PH2 = PR2 – HR2 (định lý pytago)
PH2 = 25- 9 = 16=> PH = 4cm
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR. Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
∆PHM vuông góc tại H nên HM2 = PM2 – PH2 (định lý pytago)
=> HM2 = 20,25 – 16 = 4, 25
=> HM = 2,1cm
Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm
Vì HM < HR => M nằm giữa H và R hay hai điểm này nằm trên cạnh QR, và nằm khác phía đối với điểm H

* Vẽ hình:
- Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6cm.
+ Vẽ đoạn thẳng QR = 6cm.
+ Vẽ cung tròn tâm Q và cung tròn tâm R bán kính 5cm. Hai cung tròn này cắt nhau tại P.
+ Nối PQ và PR ta được tam giác cần vẽ.
- Vẽ điểm M : Vẽ cung tròn tâm P bán kính 4,5cm cắt QR (nếu có) tại M.
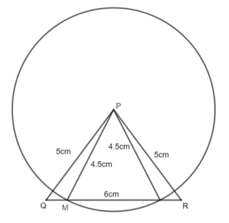
Vậy ta có thể vẽ được 2 điểm M trên đường thẳng QR để PM = 4.5cm
* Kẻ đường cao PH của ΔPQR
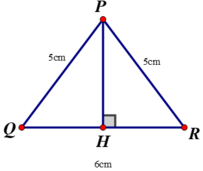
Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có
PH chung
PQ = PR ( = 5cm)
⇒ ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)
⇒ HQ = HR (Hai cạnh tương ứng)
Mà HQ + HR = QR = 6 cm
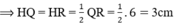
+ ΔPHR vuông tại H có PR2= PH2+ HR2(định lí Py – ta – go)
⇒ PH2= PR2– HR2= 52– 32= 16 ⇒ PH = 4cm .
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
+ Lại có : HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.
Mà PM < PR ⇒ HM < HR = HQ (đường xiên nào lớn hơn thì hình chiếu lớn hơn).
⇒ M nằm giữa H và Q hoặc H và R
⇒ M nằm trên cạnh QP và có hai điểm M như vậy.
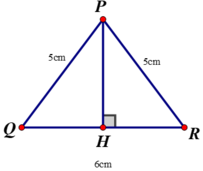

Kẻ đường cao AH của ∆PQR
=> H là trung điểm của QR
=> HR = QR = 3cm
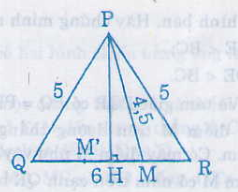
+ ∆PHR vuông tại H
nên PH2 = PR2 – HR2 (định lý pytago)
PH2 = 25- 9 = 16=> PH = 4cm
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR. Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
∆PHM vuông góc tại H nên HM2 = PM2 – PH2 (định lý pytago)
=> HM2 = 20,25 – 16 = 4, 25
=> HM = 2,1cm
Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm
Vì HM < HR => M nằm giữa H và R hay hai điểm này nằm trên cạnh QR, và nằm khác phía đối với điểm H
Kẻ đường cao AH của ∆PQR
=> H là trung điểm của QR
=> HR = QR = 3cm
∆PHR vuông tại H
Ta có: PH2 = PR2 – HR2 ( dlptg )
Hay PH2 = 25 - 9 = 16
=> PH = căn 16 = 4cm
Vậy đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
∆PHM vuông góc tại H nên
HM2 = PM2 – PH 2 (định lý pytago)
=> HM2 = 20,25 – 16 = 4,25
=> HM = căn 4,25 = 2,1cm
Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm
Do HM < HR
=> M nằm giữa H và R hay hai điểm này nằm trên cạnh QR và nằm khác phía đối với điểm H

Ta có Tam giác PQR cân tại P vì PQ=PR
Kẻ đường cao PH của Tam giác PQR ta có
Vì Tam giác PQR cân tại P => H là trung điểm RQ => HR=HQ=1/2.RQ=1/2.6=3(cm)
Tam giác PRH vuông tại H, Áp dụng ĐL Pytago có
\(PR^2=RH^2+PH^2\)
\(5^2=3^2+PH^2\)=> PH=4cm
Xét Tam giác PMH vuông tại H, áp dụng PYtago ta có
\(PM^2=PH^2+MH^2\)
\(4.5^2=4^2+MH^2\)
=> MH=\(\sqrt{4.5^2-4^2}\)
Nếu M thuộc đoạn RH (TM)
Nếu M thuộc đoạn QH (TM)
Vậy có 2 đuiểm M thảo mãn yêu cầu
(P/s) có thể Ah trình bày ko đúng lém đâu hen
_Kudo_

Kẻ đường cao AH của ∆PQR
=> H là trung điểm của QR
=> HR =\(\dfrac{1}{2}\)( cm )
QR = 3( cm )

+ ∆PHR vuông tại H
nên PH2 = PR2 – HR2 (định lý pytago)
PH2 = 25- 9 = 16=> PH = 4cm
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR. Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
∆PHM vuông góc tại H nên HM2 = PM2 – PH2 (định lý pytago)
=> HM2 = 20,25 – 16 = 4, 25
=> HM = 2,1cm
Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm
Vì HM < HR => M nằm giữa H và R hay hai điểm này nằm trên cạnh QR, và nằm khác phía đối với điểm H

Kẻ đường cao AH của ∆PQR
=> H là trung điểm của QR
=> HR = 1/2 QR = 3cm
∆PHR vuông tại H
nên PH2 = PR2 – HR2 (định lý pytago)
PH2 = 25- 9 = 16=> PH = 4cm
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR. Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
∆PHM vuông góc tại H nên HM2 = PM2 – PH2 (định lý pytago)
=> HM2 = 20,25 – 16 = 4, 25
=> HM = 2,1cm
Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm
Vì HM < HR => M nằm giữa H và R hay hai điểm này nằm trên cạnh QR, và nằm khác phía đối với điểm H

Kẻ đường cao AH của ∆PQR
=> H là trung điểm của QR
=> HR =\(\dfrac{1}{2}\) QR = 3cm
+ ∆PHR vuông tại H
nên PH2 = PR2 – HR2 (định lý pytago)
PH2 = 25- 9 = 16=> PH = 4cm
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR. Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
∆PHM vuông góc tại H nên HM2 = PM2 – PH2 (định lý pytago)
=> HM2 = 20,25 – 16 = 4, 25
=> HM = 2,1cm
Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm
Vì HM < HR => M nằm giữa H và R hay hai điểm này nằm trên cạnh QR, và nằm khác phía đối với điểm H
Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có
PH chung
PQ = PR ( = 5cm)
⇒ ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)
⇒ HQ = HR (Hai cạnh tương ứng)
Mà HQ + HR = QR = 6 cm
+ ΔPHR vuông tại H có PR2= PH2+ HR2(định lí Py – ta – go)
⇒ PH2= PR2– HR2= 52– 32= 16 ⇒ PH = 4cm .
Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.
+ Lại có : HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.
Mà PM < PR ⇒ HM < HR = HQ (đường xiên nào lớn hơn thì hình chiếu lớn hơn).
⇒ M nằm giữa H và Q hoặc H và R
⇒ M nằm trên cạnh QP và có hai điểm M như vậy.
có 2 điểm M
Và 2 điểm M đó có nằm trên QR