Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 10. Vẽ một tam giác vuông có một góc nhọn 34∘34∘ rồi viết các tỉ số lượng giác của góc 34∘34∘.
Hướng dẫn giải:
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
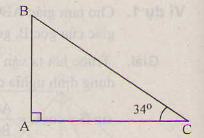
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.
Xem thêm tại: http://loigiaihay.com/bai-10-trang-76-sgk-toan-9-tap-1-c44a2814.html#ixzz4rLOPb3I0

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:
sin60° = cos(90° – 60°) = cos30°
Tương tự:
cos75° = sin(90° – 75°) = sin 15°
sin52°30′ = cos(90° – 52°30′) = 38°30′
cotg82° = tg8°; tg80° = cotg10°

Làm tiêu biểu 1 bài thôi nhé. Các bài còn lại tương tự
a/ sin a = 0,8
Ta có: sin2 a + cos2 a = 1
=> cos2 a = 1 - sin2 a = 1 - 0,82 = 0,36
\(\Rightarrow\orbr{\begin{cases}cos\:a=0,6\\cos\:a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tan\:a=\frac{4}{3}\\tan\:a=-\frac{4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}cot\:a=\frac{3}{4}\\cot\:a=-\frac{3}{4}\end{cases}}\)

Gọi cạnh huyền là a, cạnh đối diện góc 300 là c, cạnh còn lại là b
Tính được \(b=c.\cot30=c\sqrt{3}\) nên \(a=\sqrt{b^2+c^2}=\sqrt{\left(c\sqrt{3}\right)^2+c^2}=2c\)
Bán kính đường tròn ngoại tiếp là R = a/2 = 2c/2 = c
Bán kính đường tròn nội tiếp là
\(r=\frac{S}{p}=\frac{bc}{2p}=\frac{bc}{a+b+c}=\frac{c^2\sqrt{3}}{2c+c\sqrt{3}+c}=\frac{c^2\sqrt{3}}{\left(3+\sqrt{3}\right)c}=\frac{\left(\sqrt{3}-1\right)c}{2}\)
Do đó \(\frac{R}{r}=c.\frac{2}{\left(\sqrt{3}-1\right)c}=1+\sqrt{3}\)
bạn thi vio à kết bạn vs mk nhé


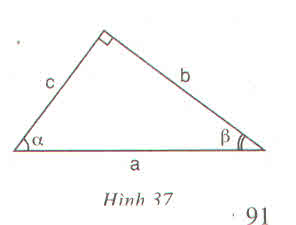

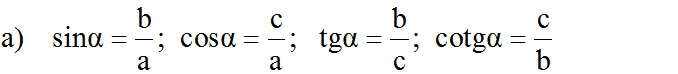
Vẽ tam giác ABC vuông tại A, góc C = 34°
Theo định nghĩa ta có:
Hướng dẫn giải:
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.