Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 (Bạn tự vẽ hình giùm)
a) Mình xin chỉnh lại đề một chút: \(\Delta ABD=\Delta ACD\)
\(\Delta ABD\)và \(\Delta ACD\)có: AB = AC (\(\Delta ABC\)cân tại A)
BD = DC (D là trung điểm của BC)
Cạnh AD chung
=> \(\Delta ABD=\Delta ACD\) (c. c. c) (đpcm)
b) Ta có \(\Delta ABD=\Delta ACD\)(cm câu a) => \(\widehat{BAD}=\widehat{DAC}\)(hai góc tương ứng) => AD là tia phân giác của \(\widehat{BAC}\)(đpcm)
c) Mình xin chỉnh lại đề một chút: AD \(\perp\)BC tại D
Ta có \(\Delta ABD=\Delta ACD\)(cm câu a) => \(\widehat{BDA}=\widehat{CDA}\)(hai góc tương ứng)
Mà \(\widehat{BDA}+\widehat{CDA}\)= 180o (kề bù)
=> \(\widehat{BDA}=\widehat{CDA}=\frac{180^o}{2}\)= 90o => AD \(\perp\)BC tại D (đpcm)

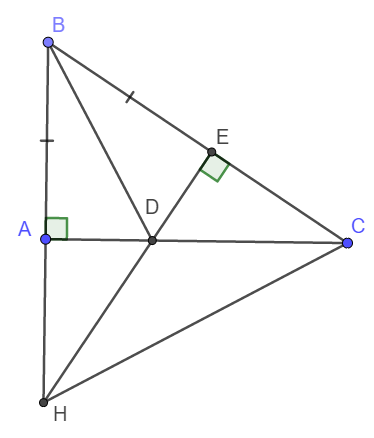
a) Xét tam giác vuông ABD và tam giác vuông EBD có:
Cạnh BD chung
BA = BE (gt)
\(\Rightarrow\Delta ABD=\Delta EBD\) (Cạnh huyền - cạnh góc vuông)
b) Do \(\Delta ABD=\Delta EBD\Rightarrow AD=ED\)
Xét tam giác vuông ADH và tam giác vuông EDC có:
AD = ED
\(\widehat{ADH}=\widehat{EDH}\)
\(\Rightarrow\Delta ADH=\Delta EDH\) (Cạnh góc vuông, góc nhọn kề)
c) Do \(\Delta ADH=\Delta EDH\Rightarrow AH=EH\)
Lại có BA = BE nên BH = BA AH = AE + EC = BC
Xét tam giác HBC có BH = BC nên HBC là tam giác cân.
Giải nhanh mình k
Mình có tận 4 nick
a, xét \(\Delta IBA\)và \(\Delta ICA\)có:
AI cạnh chung
\(\widehat{IAB}\)=\(\widehat{IAC}\)(vì AI là phân giác)
AB=AC(gt)
=> \(\Delta IBA=\Delta ICA\)(c.g.c)
A B C I