Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

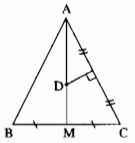
∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
D là giao điểm của các đường trung trực AC và BC nên D thuộc trung trực của AB.
Vậy DA = DB (tính chất đường trung trực).

Vì ∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
Vì D là giao điểm của các đường trung trực AC và BC nên D thuộc đường trung trực của AB.
Theo tính chất đường trung trực, ta có:
DA = DB.

_Giải _
a) C/m t/g AMC cân tại M
* Xét t/g AMN và t/g CMN :
- AN = CN ( N là trung điểm )
- Góc ANM = CNM ( = 900 do MN là trung trực đoạn AC )
- MN chung
=> T/g AMN = T/g CMN
=> MA = MC
=> T/g AMC cân tại M
b ) Em hông biết làm .. T.T Thông cẻm nhe :)))))

Vì D nằm trên đường trung trực của AC
nên DA=DC(1)
Xét ΔDBC có
DM là đường cao
DM là đường trung tuyến
Do đó;ΔDBC cân tại D
=>DB=DC(2)
Từ (1) và (2) suy ra DA=DB

Xét tam giác amc = tam giác dmb có:
cạnh mc = mb[ giả thiết]
góc amc =dmb[2 góc đối đỉnh]
ta có bd song song với ac nên suy ra góc acm = góc mbd
=> tam giác amc = tam giác dmb [ g.c.g]

A B C M
a) Xét t/giác ABM và t.giác ACM
có: AB = AC (gt)
AM : chung
BM = MC (gt)
=> t/giác ABM = t/giác ACM (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc t/ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=90^0\)
=> AM vuông góc với BC
b) Ta có: BM = MC = 1/2BC = 1/2.32 = 16 (cm)
Áp dụng định lí Pi - ta - go vào t/giác ABM vuông tại M, ta có:
\(AB^2=AM^2+BM^2\)
=> AM2 = AB2 - BM2 = 342 - 162 = 900
=> AM = 30 (cm)
c) Chu vi t/giác AMB = 34 + 16 + 30 = 80 (cm)
Diện tích t/giác ABM là: 30 x 16 : 2 = 240 (cm2)
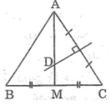
a: Xét ΔAMB và ΔAMC có
AM chung
AB=AC
MB=MC
=>ΔAMB=ΔAMC
b: Xét ΔDMB vuông tạiM và ΔDMC vuông tại M có
DM chung
MB=MC
=>ΔDMB=ΔDMC
c: ΔDMB=ΔDMC
=>DB=DC
D nằm trên trung trực của AC
=>DA=DC=DB