Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Thấu kính dịch ra xa vật thì ảnh
dịch lại gần thấu kính. Vì thấu kính rời lại gần màn thêm 15 cm đồng thời màn cũng dời lại gần thấu kính thêm 15 cm nên:



a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!

Sơ đồ tạo ảnh:
![]()
a) Vì vật là vật thật, qua thấu kính cho ảnh thật nên thấu kính phải là thấu kính hội tụ. Ảnh dịch chuyển ra xa thấu kính.


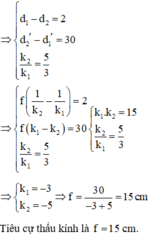

Đáp án cần chọn là: C
Gọi khoảng cách của vật tới thấu kính trước khi dịch chuyển là d, khoảng cách ảnh tới thấu kính là d’ ta có: 1 d 1 + 1 d 1 ' = 1 f = 1 10 (1)
Với thấu kính hội tụ khi dịch chuyển vật một khoảng 5cm lại gần thấu kính thì ảnh sẽ dịch chuyển xa thấu kính hơn, theo đề bài ảnh dịch chuyển một khoảng là 10cm nên ta có: 1 d 2 + 1 d 2 ' = 1 f
→ 1 d 1 − 5 + 1 d 1 ' + 10 = 1 10 (2)
Từ (1) và (2) → d 1 = 20 c m ; d 1 ' = 20 c m

(đề bài), ...và cách thấu kính 12cm à (hình anh tự vẽ )
\(=>d< f\left(12cm< 20cm\right)\)=>ảnh tạo bới vật AB qua thấu kính hội tụ là ảnh ảo , lớn hơn vật và cùng chiều vật
\(=>\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}=>\dfrac{1}{20}=\dfrac{1}{12}-\dfrac{1}{d'}=>d'=30cm\)
=>ảnh cách tk 30cm
\(=>\dfrac{h}{h'}=\dfrac{d}{d'}=>\dfrac{2}{h'}=\dfrac{12}{30}=>h'=5cm\)
=>ảnh A'B' cao 5cm
\(=>\)khoảng cách giữa ảnh với vật d+d'=42cm

Sơ đồ tạo ảnh:
![]()
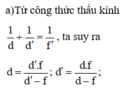
Số phóng đại ảnh qua thấu kính: k = − d ' d
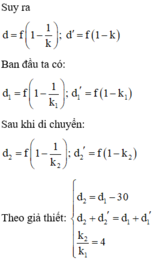
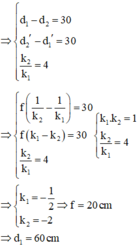
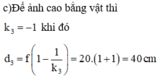
Như vậy để có ảnh cao bằng vật thì cần dịch chuyển vật lại gần thấu kính một đoạn 60 - 40 = 20 cm


Ta có hệ là ảnh thật
\(\Rightarrow d'>0\\ \Leftrightarrow\left\{{}\begin{matrix}d+d'=45\\\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d+d'=45\\\dfrac{d+d'}{d.d'}=\dfrac{1}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d+d'=45\\d.d'=450\end{matrix}\right.\)
Áp dụng Vi ét ta có d & d' là no của pt
\(x^2-45x+450=0\Leftrightarrow\left\{{}\begin{matrix}x_1=15\\x_2=30\end{matrix}\right.\)
Ảnh > vật ( d > d' )
\(\Rightarrow d'=30,d=15\)
b, Kcách từ ảnh đến vật là d' + d = s
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\Rightarrow d'=\dfrac{df}{d-f}\Rightarrow s=d+\dfrac{df}{df}\\ s'd=1+\dfrac{f\left(d-f\right)-df}{\left(d-f\right)^2}=1-\dfrac{f^2}{\left(d-f\right)^2}\)
Tại \(d=15\Rightarrow s'd\left(15\right)=-3\)
--> d tăng s giảm
--> ảnh dịch lại gần vật
hệ thức Vi-ét làm gì dợ Châu bà giải delta là ra gòi:v ( mà cái này có Vi-ét à ?? ):))